What is a model?

The word model refers to a representation, often simplified, of an object or of an observation. A model is thus expected to at least mimic, but preferably explain and predict relevant aspects of a given phenomenon. A mathematical model typically consists of one or more equations relating dependent (or output) to independent (or input) variables. Often, a mathematical model involves parameters.

This definition raises the question of reproduction versus explanation. Consider for instance the formation of ripples on a sandy beach. One could imagine developing a model which would take into account how each particle of sand interacts with its neighbors, with the surrounding air, and with particles at rest on the ground. This would be a fairly complicated model, which would involve many dynamical equations, but which should, under appropriate circumstances, be able to reproduce the formation of sand ripples. Another approach could be at a more global level. One could then imagine a model that considers the elevation of the sand on the ground and shows that, in some parameter regime, this quantity oscillates as a function of space. Both models would reproduce the desired phenomenon, but would provide different types of explanation. This is due to the difference in their nature: the former is a model at the microscopic or particulate level, the latter is a model at the macroscopic level. A third model could be a sort of “black box,” whose input would be relevant parameters such as the speed of the wind, and the mass and size of the particles of sand, and whose output would be a stripe pattern with the correct properties (period, height, etc). One could create such a model by conducting careful experiments, tabulating the results, and finding functions that fit the data. This model would not offer an explanation as to why sand ripples form, but could still have some predictive capabilities.

Along the same lines, it is well-known that mountains, clouds, trees or even some artistic works resemble fractals. Recognizing this fact may help graphic designers create convincing and aesthetically pleasing virtual landscapes, but does not for instance explain how mountains or clouds are formed.

Different models may thus produce similar results, and modelers need to decide which model best suits their needs. This is of course a subjective task, the  outcome of which should be based on the answers to the following questions.

• What do we want the model to do: reproduce, explain, predict, etc?
• Is a predictive but costly model worth the effort invested in its creation?
• What minimal  set of criteria should the model satisfy?

A related issue is that different phenomena may lead to similar behaviors (a little like different diseases may have similar symptoms). As a consequence, a model which reproduces the desired behaviors may not have any explanatory or predictive value (similarly, one cannot reasonably diagnose a disease based on symptoms that are not unique to this particular disease).

In this text, we will not consider curve-fitting approaches (although see the exercises for applications of the least squares method), but focus our attention on models that are descriptive and explanatory. Such models will often consist of a collection of dynamical equations. We will discuss how to analyze them, in order to assess their ability to reproduce and predict relevant phenomena. We will assume the reader has a working knowledge of calculus, differential equations and linear algebra. Brief reviews of these topics are provided in the appendices.

How to develop a mathematical model

We now turn to the basic steps involved in the creation of a mathematical model. We will follow these guidelines in all of the models discussed here, very explicitly at first, and then in a more implicit fashion.

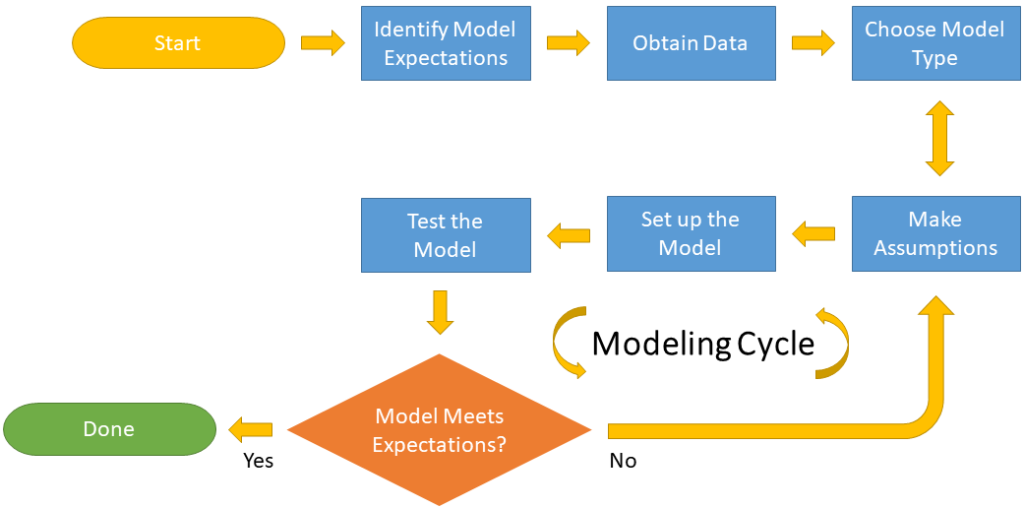
Identify what we want to model

The first step is to decide what the model should accomplish. In other words, we need to find a set of criteria that a satisfactory model should meet. These criteria typically result from balancing the desire of having a perfect model against any time and cost constraints associated with creating such a model.

Obtain data

This is often the best way to develop an intuitive understanding of the phenomenon of interest. If appropriate, we should also master the basic physical, biological or chemical principles that are responsible for the observed behavior. This may be fairly involved, and often requires finding information in the literature and/or discussing the data with experts.

Choose the level of complexity of the model

Going back to the example of the formation of sand ripples discussed above, we should for instance decide whether a microscopic model should be preferred to a macroscopic model. Such a decision may be based on personal taste, on the nature of available data, and on the current level of understanding of the phenomenon.

Make assumptions

We have to decide which facts (or parameters) are irrelevant and therefore negligible, and which ones have to be taken into account.

Set up the model

We need to define the independent and dependent variables, define the relevant parameters, and write a mathematical formulation of the model. This formulation should be as simple as possible, and we should have a clear understanding of the significance of each of the terms that appear in the equations forming the mathematical model.

Test the model

This is a crucial step in deciding whether we are satisfied with our model. The behavior of the model may be investigated analytically, or numerically, or both. We then have to ask ourselves whether our intuition generally agrees with what the model does, whether the model is qualitatively and quantitatively correct, and whether limiting cases make sense. If not, we need to find why and amend the model accordingly – in other words, we need to go back to the previous steps. This is thus an iterative process, illustrated in Figure 1.1, during which the model is perfected by testing the results of our analysis of the model against our intuition, against available experimental data, or against the accepted understanding of the phenomenon under study.

Why develop mathematical models

A mathematical model is a set of equations that reflects our understanding of a given phenomenon. It may look mysterious to the neophyte, but for someone who knows how to read a model, it is an efficient and concise means of communication. A lot of effort, thinking, testing and understanding goes into the creation of a model, but in the end, all this work is summarized by a set of equations or by the formulation of some iterative process. Such a model is a scientists’ expression of their perception of the world.

Models have also more practical purposes. They may be used to describe or investigate limiting situations which cannot be reached in practice. In particular, the different ingredients of a model may be isolated from one another by setting all parameters but a few to zero. Models also allow us to save time and resources. For instance, computer simulations of car crashes are cheaper than performing actual experiments. Flight simulators are used as training devices. Models may be run as part of feasibility studies, or to test the outcome of various possible scenarios.

Because models are increasingly used to make decisions that impact society (see for instance the news articles listed in Problem 2 at the end of this chapter), it is important to know their limitations, to realize which hypotheses they are based upon, and to know the role, which may be crucial, that these hypotheses play in the model. An article by R. May, entitled Uses and Abuses of Mathematics in Biology, further reflects on such issues.

What does it take to be a good modeler?

Mathematical modeling combines various areas of mathematics (for instance differential equations, calculus, linear algebra, numerical analysis, probability theory, dynamical systems, statistics, uncertainty quantification) with, depending on the nature of the model, knowledge of physics, biology, chemistry, astrophysics, geology, hydrology, etc. These subjects are typically taught independently from one another, and the main instructional goal of a mathematical modeling course is to discuss how to draw on various areas of knowledge in order to build and analyze a model. As a consequence, a reader well trained in mathematics and other scientific disciplines will find that there is no “new material” in these notes. What is new is the use of a variety of mathematical tools to reach a single objective: develop, understand, and test mathematical models.

Successful mathematical modeling thus requires some sort of resourcefulness, since the modeler should be able to “think” of the right tools or methods to use. It also requires some curiosity, imagination and patience; an ability to understand problems that are not purely mathematical; an ability to simplify a given problem, in order to decide what is relevant and what is not; an ability to turn concepts into equations, to decide whether a model is good or inadequate; and finally an ability to discuss problems with others, particularly those whose expertise is different from one’s own.

Summary

The phrase mathematical modeling may be understood in a variety of ways. In these notes, only models that are explanatory, predictive, and have a mathematical formulation qualify as mathematical models. In particular, curve fitting techniques or statistical models are not discussed.

The modeling process involves a series of steps that modelers need to go through in a systematic fashion. These include knowing what one wants to model, getting data, deciding on the type of model to be developed, making assumptions, constructing the model, testing and amending it, and finally using the model. It is particularly important that simplifying hypotheses made in the development of the model be clearly understood, especially if the results are used for policy or decision making purposes.

Mathematical modeling is an interdisciplinary activity which requires an appreciation for the power of mathematical analysis, an interest in applied disciplines, a solid mathematical and computational background, as well as good communication skills.