9 Diffusion
Learning Objectives
At the end of this chapter, you will be able to do the following.
- Construct continuity equations using ideas from vector calculus.
- Interpret reaction-diffusion equations as special cases of continuity equations.
- Solve the heat equation.
- Describe diffusion at the microscopic level.
- Compare diffusive processes at the microscopic and macroscopic levels.
- Justify the existence of a traveling wave solution to the Fisher-KPP equation.
Diffusion at the macroscopic level
Reaction-diffusion equations
Consider a quantity [latex]F(x,y,z,t)[/latex], which depends on the three space variables [latex]x[/latex], [latex]y[/latex], and [latex]z[/latex], as well as time [latex]t.[/latex] Assume that [latex]F[/latex] measures the density of some species, in number of individuals per unit volume. A similar treatment would apply to the number of individuals per unit area in a two-dimensional model, or per unit length in a one-dimensional model. We are interested in describing the evolution of [latex]F[/latex].
Consider a closed region of space [latex]\Omega[/latex], and call [latex]N_i[/latex] the number of individuals inside [latex]\Omega[/latex]. From the definition of [latex]F[/latex], we know that
[latex]\displaystyle N_i = \iiint_\Omega F(x,y,z,t)\ dV,[/latex]
where [latex]d V[/latex] denotes the volume element in [latex]\Omega[/latex]. Let us evaluate the time derivative of [latex]N_i[/latex]. We will assume that [latex]F[/latex] is regular enough to allow us to swap the derivative and integral signs, so that
[latex]\displaystyle \frac{d N_i}{d t} = \frac{d}{d t} \iiint_\Omega F(x,y,z,t)\ dV = \iiint_\Omega \frac{\partial F}{\partial t}\ dV. \qquad (9.1)[/latex]
On the other hand, the change in [latex]N_i[/latex] should reflect the local variations of [latex]N_i[/latex], as well as transport through the boundary [latex]\partial \Omega[/latex] of [latex]\Omega[/latex]. We thus have
[latex]\displaystyle \frac{d N_i}{d t} = \iiint_\Omega R(x,y,z,t,F)\ dV - \iint_{\partial \Omega} \vec \jmath (\vec r) \cdot \vec n \ dS, \qquad (9.2)[/latex]
where [latex]R[/latex] is a reaction term describing the local change in [latex]F[/latex], [latex]\vec r[/latex] is the position vector, [latex]\vec n[/latex] is the normal to [latex]\Omega[/latex] pointing outwards, [latex]dS[/latex] is the surface element on [latex]\partial \Omega[/latex], and [latex]\vec \jmath[/latex] is a vector describing the flow of [latex]N_i[/latex]. The last term in (9.2) is the negative of the flux of [latex]\vec \jmath[/latex] through the boundary of [latex]\Omega[/latex]. The negative sign comes from the fact that [latex]\vec n[/latex] point outwards, and that individuals leaving [latex]\Omega[/latex] contribute to a decrease in [latex]N_i[/latex]. With the divergence theorem (again, we implicitly assume all quantities have enough regularity) this term can be re-written as
[latex]\displaystyle - \iint_{\partial \Omega} \vec \jmath(\vec r) \cdot \vec n \ dS = - \iiint_\Omega \vec \nabla \cdot \vec \jmath\ dV,[/latex]
so that
[latex]\displaystyle \frac{d N_i}{d t} = \iiint_\Omega \left[R(x,y,z,t,F) - \vec \nabla \cdot \vec \jmath \right] \ dV. \qquad (9.3)[/latex]
By combining Equations (9.1) and (9.3), we get
[latex]\displaystyle 0 = \iiint_\Omega \left[-\frac{\partial F}{\partial t} + R(x,y,z,t) - \vec \nabla \cdot \vec \jmath \right] \ dV.[/latex]
Since this equality is true for an arbitrary closed domain [latex]\Omega[/latex], we obtain the following continuity equation
[latex]\displaystyle \frac{\partial F}{\partial t} = R(x,y,z,t,F) - \vec \nabla \cdot \vec \jmath, \qquad (9.4)[/latex]
which describes the conservation of [latex]F[/latex]. We now have to relate [latex]\vec \jmath[/latex] to [latex]F[/latex]. As a first approximation, we will assume that Fick's law is valid, i.e. that [latex]\vec \jmath[/latex] only depends on the gradient of [latex]F[/latex],
[latex]\vec \jmath = - D \, \vec \nabla F,[/latex]
where the diffusion tensor [latex]D[/latex] is a matrix of diffusion coefficients. The entries of [latex]D[/latex] may depend on [latex]F[/latex], in which case we have nonlinear diffusion. Depending on the properties of the medium, [latex]D[/latex] may not be diagonal or even isotropic. In what follows, me make the simplifying assumption that [latex]D = D_0 I_3[/latex], where [latex]I_3[/latex] is the [latex]3 \times 3[/latex] identity matrix, and [latex]D_0[/latex] is a constant. We thus have that [latex]\vec \jmath[/latex] is proportional to the gradient of [latex]F[/latex],
[latex]\vec \jmath = - D_0 \vec \nabla F. \qquad (9.5)[/latex]
Here [latex]D_0[/latex] is positive, which describes the fact that [latex]F[/latex] ``moves away'' from regions regions of high concentration, towards regions of low concentration. By combining (9.4) with (9.5), we obtain the following reaction-diffusion equation,
[latex]\displaystyle \frac{\partial F}{\partial t} = R(x,y,z,t,F) + D_0 \Delta F, \qquad (9.6)[/latex]
where [latex]\Delta = {\vec \nabla}^2[/latex] denotes the Laplacian. If [latex]F[/latex] and [latex]R[/latex] are uniform, i.e. [latex]F(x,y,z,t) = G(t)[/latex] and [latex]R(x,y,z,t,F) = H(t,G)[/latex], then Equation (9.6) reduces to an ordinary differential equation,
[latex]\displaystyle \frac{d G}{d t} = H(t,G),[/latex]
where [latex]H[/latex] can for instance be the logistic model, [latex]H(t,G) = G (1 - G)[/latex]. We can thus extend all of the models discussed before by converting systems of ordinary differential equations into systems of partial differential equations, with appropriate diffusion terms.
The heat equation
In the absence of reaction terms, Equation (9.6) becomes the heat equation,
[latex]\displaystyle \frac{\partial F}{\partial t} = D_0 \Delta F. \qquad (9.7)[/latex]
This is a linear equation in [latex]F[/latex]. If appropriate initial and boundary conditions are supplied, a unique solution can be found in terms of Green's functions. On an infinite domain for instance, the solution to (9.7) with initial condition [latex]F(x,y,z,0) = H(x,y,z)[/latex] is
[latex]\displaystyle F(x,y,z,t)= \left(\frac{1}{4 \pi D_0 t}\right)^{3/2} \int_{-\infty}^\infty \int_{-\infty}^\infty \int_{-\infty}^\infty \exp\left[- \frac{|\vec r - \vec \mu|^2}{4 D_0 t}\right] H(\xi,\zeta,\eta)\, d \xi\, d \zeta \, d \eta,[/latex]
where
[latex]|\vec r - \vec \mu|^2 = (x-\xi)^2 + (y - \zeta)^2 + (z - \eta)^2.[/latex]
From a dimensional analysis point of view, we know that
[latex]\left[ D_0 \right] = \frac{L^2}{T}.[/latex]
As a consequence, one expects the square of characteristic length scales of the problem to vary like characteristic time scales.
Diffusion at the microscopic level
A microscopic description of diffusion is as follows. Consider for instance a collection of molecules in a fluid, such as molecules of dye in water. If the temperature is non-zero, these molecules move randomly, and undergo what is called Brownian motion. What we call diffusion at the macroscopic level is the consequence of random motion at the microscopic level. To make this more intuitive, consider a particle undergoing a random walk in the plane: each step has a given length [latex]l[/latex], but can be taken in a random, uniformly distributed, direction. After [latex]N[/latex] steps, of equivalently a time [latex]T = N \delta t[/latex], where [latex]\delta t[/latex] is the time elapsed between any two consecutive steps, the particle will be at a distance [latex]L[/latex] from its original position, such that
[latex]\langle L^2 \rangle = N l^2.[/latex]
To see this, call [latex]\vec r_i[/latex] the position vector of the particle after [latex]i[/latex] steps. Assume for simplicity that the particle started its walk from the origin. Since each step has length [latex]l[/latex],
[latex]|\vec r_1|^2 = l^2, \qquad \hbox{and} \qquad \langle |\vec r_1|^2 \rangle = l^2,[/latex]
where the average [latex]\langle \cdot \rangle[/latex] is taken over all possible realizations of the particle taking one step. We will show by induction that after [latex]k[/latex] steps, [latex]k \in \mathbb{N}[/latex], we have
[latex]\langle |\vec r_k|^2 \rangle = k\, l^2.[/latex]
We know this statement is true for [latex]k = 1[/latex]. We now show that if it is true for [latex]k = n[/latex], then it is also true for [latex]k = n+1[/latex]. We thus assume that
[latex]\langle |\vec r_n|^2 \rangle = n\, l^2,[/latex]
and calculate [latex]\langle|\vec r_{n+1}|^2\rangle[/latex]. We have
[latex]\begin{array}{l}|\vec r_{n+1}|^2 &= |[\vec r_n + (\vec r_{n+1}-\vec r_n)]|^2 \\ &= |\vec r_n|^2 + 2 \vec r_n \cdot (\vec r_{n+1}-\vec r_n) + |(\vec r_{n+1}-\vec r_n)|^2.\end{array}[/latex]
But
[latex]\vec r_{n+1} - \vec r_n = l\, [\cos(\theta_{n+1}) \vec \imath + \sin(\theta_{n+1}) \vec \jmath],[/latex]
where [latex](\vec \imath, \vec \jmath)[/latex] is an orthonormal basis of the plane, and the angle [latex]\theta_{n+1}[/latex] is uniformly distributed. As a consequence,
[latex]\begin{array}{ll} \langle \vec r_n \cdot (\vec r_{n+1}-\vec r_n) \rangle &= l\, (\vec r_n \cdot \vec \imath) \langle \cos(\theta_{n+1}) \rangle + l\, (\vec r_n \cdot \vec \jmath) \langle \sin(\theta_{n+1}) \rangle \\ &= 0, \end{array}[/latex]
and [latex]|(\vec r_{n+1}-\vec r_n)|^2 = l^2[/latex]. Thus,
[latex]\langle |\vec r_{n+1}|^2 \rangle = \langle |\vec r_n|^2 \rangle + 0 + l^2 = (n+1)\, l^2.[/latex]
Therefore, [latex]\langle |\vec r_k|^2 \rangle = k\, l^2[/latex] for any positive integer [latex]k[/latex]. Thus [latex]\langle L^2 \rangle = N l^2[/latex] and since [latex]T = N \delta t[/latex], we have [latex]\langle L^2 \rangle \propto T[/latex].
Consider the following experiment. Many non-interacting particle are simultaneously released at the origin, and each particle performs an isotropic random walk in the plane. The above calculation tells us that after a period of time [latex]T[/latex], we expect to see a cloud of particles, and that if we measure the distance [latex]L[/latex] between each particle and the origin, we should find that [latex]\langle L^2 \rangle \propto T.[/latex]
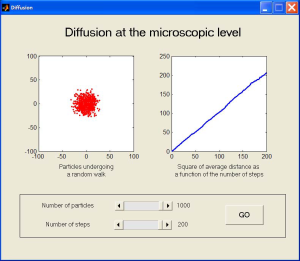
To provide a visual understanding of this result, the Diffusion MATLAB GUI (see Figure 9.1) simulates the random motion of [latex]M[/latex] non-interacting particles on a grid - so that each particle can only go up, down, left or right, with equal probability. All of the particles star their random walk from the origin, at the center of the box. For each particle, the distance [latex]L[/latex] between its position after [latex]N[/latex] steps (or equivalently after a time [latex]T = N \delta t[/latex], where [latex]\delta t[/latex] is fixed) and the origin is measured as a function of [latex]N[/latex]. The result is averaged over all of the particles, and plotted. The user can choose the maximum number of steps, [latex]N_{max}[/latex], as well as the number of particles [latex]M[/latex]. The interface shows the position of all of the particles as time evolves. One of the particles is marked in blue, so that the user can follow its random walk. At the end of the simulation, a plot of the average of [latex]L^2[/latex] is shown as a function of [latex]N[/latex].
This simulation suggests that diffusion as modeled by the heat equation at the macroscopic level can be understood as resulting from the random walk of independent particles at the microscopic level. These two phenomena indeed have the same scaling properties. This correspondence can in fact be made rigorous, but we will not discuss this here. It is however useful to keep in mind the microscopic description of diffusion. Indeed, we often tend to develop macroscopic models based on our understanding of behaviors at the microscopic level. It is thus important to know under which conditions a particular phenomenon may be adequately modeled at the macroscopic level by diffusive terms.
The Fisher-Kolmogorov-Petrovsky-Piscounov equation
We now turn to a simple example of a one-dimensional reaction-diffusion equation, known as the Fisher-Kolmogorov-Petrovsky-Piscounov (Fisher-KPP) equation.[1][2] Consider the one-dimensional version of the logistic equation with diffusion,
[latex]\displaystyle \frac{\partial N}{\partial t} = r N \left(1 - \frac{N}{K} \right) + D \frac{\partial^2 N}{\partial X^2},[/latex]
where [latex]r[/latex], [latex]K[/latex] and [latex]D[/latex] are constant. This equation can be made dimensionless by scaling space, time and the dependent variable [latex]N[/latex]. To this end, we define
[latex]\displaystyle n = \frac{N}{K}, \qquad x = X \sqrt \frac{r}{D}, \qquad y = Y\sqrt \frac{r}{D}, \qquad \tau = r\, t,[/latex]
and obtain the dimensionless Fisher-KPP equation,
[latex]\displaystyle \frac{\partial n}{\partial \tau} = n \left(1 - n \right) + \frac{\partial^2 n}{\partial x^2}. \qquad (9.8)[/latex]
This equation has been widely studied in the literature[3], and we only mention below one of its properties, namely that it admits a family of traveling wave solutions defined on the real line.
Equation (9.8) has two uniform and constant solutions, given by [latex]n = 0[/latex] and [latex]n = 1[/latex], and we can look for a traveling wave solution connecting these two solutions. To do so, we set [latex]n(x,t) = v (\xi)[/latex], where [latex]\xi = x - c t[/latex] and the speed [latex]c[/latex] is arbitrary, and substitute into (9.8). Using the chain rule, we obtain
[latex]\displaystyle \frac{\partial n}{\partial t} = - c \frac{d v}{d \xi}, \qquad \frac{\partial n}{\partial x} = \frac{d v}{d \xi},[/latex]
so that [latex]v[/latex] satisfies the ordinary differential equation
[latex]\displaystyle \frac{d^2 v}{d \xi^2} + c \frac{d v}{d \xi} + v (1 - v) = 0. \qquad (9.9)[/latex]
The dynamics of this equation may be qualitatively described by looking at the corresponding phase plane. Let [latex]\frac{d v}{d \xi} = w[/latex]. Then,
[latex]\displaystyle \frac{d w}{d \xi} = \frac{d^2 v}{d \xi^2} = - c w - v (1 - v),[/latex]
and (9.9) is equivalent to the following dynamical system
[latex]\displaystyle \frac{d}{d \xi} \left(\begin{array}{c}v \\ w\end{array} \right) = \left( \begin{array}{c} w \\ - c w - v (1 - v) \end{array} \right). \qquad (9.10)[/latex]
Its fixed points in the [latex](v,w)[/latex] plane are are [latex]P_0 = (0,0)[/latex] and [latex]P_1 = (1,0)[/latex]. The Jacobian is
[latex]J(v,w) = \left(\begin{array}{cc} 0 & 1 \\ - 1 + 2 v & - c \end{array}\right),[/latex]
and
[latex]J(0,0) = \left(\begin{array}{cc} 0 & 1 \\ - 1 & - c \end{array}\right), \qquad J(1,0) = \left(\begin{array}{cc} 0 & 1 \\ 1 & - c \end{array}\right).[/latex]
For [latex]P_1[/latex], [latex]\det(J(P_1)) = -1[/latex], so that [latex]P_1[/latex] is a saddle. The origin has eigenvalues[latex]\lambda_1[/latex] and [latex]\lambda_2[/latex] with [latex]\lambda_1 \lambda_2 = 1 > 0[/latex] and [latex]\lambda_1 + \lambda_2 = - c[/latex]. We can assume without loss of generality that [latex]c[/latex] is non-negative, since changing [latex]c[/latex] into [latex]-c[/latex] is the same as changing [latex]\xi[/latex] into [latex]-\xi[/latex] in Equation (9.9). If [latex]c = 0[/latex], the origin is a center. If [latex]c > 0[/latex], the origin is either a stable node or a stable spiral. Since [latex]P_1[/latex] is a saddle and the origin a node or a spiral, there is, for each value of [latex]c > 0[/latex], a trajectory which connects [latex]P_1[/latex] to [latex]P_0[/latex]. This corresponds to a front, moving at speed [latex]c[/latex], and describing the growth of [latex]n = 1[/latex] into a region with [latex]n = 0[/latex].
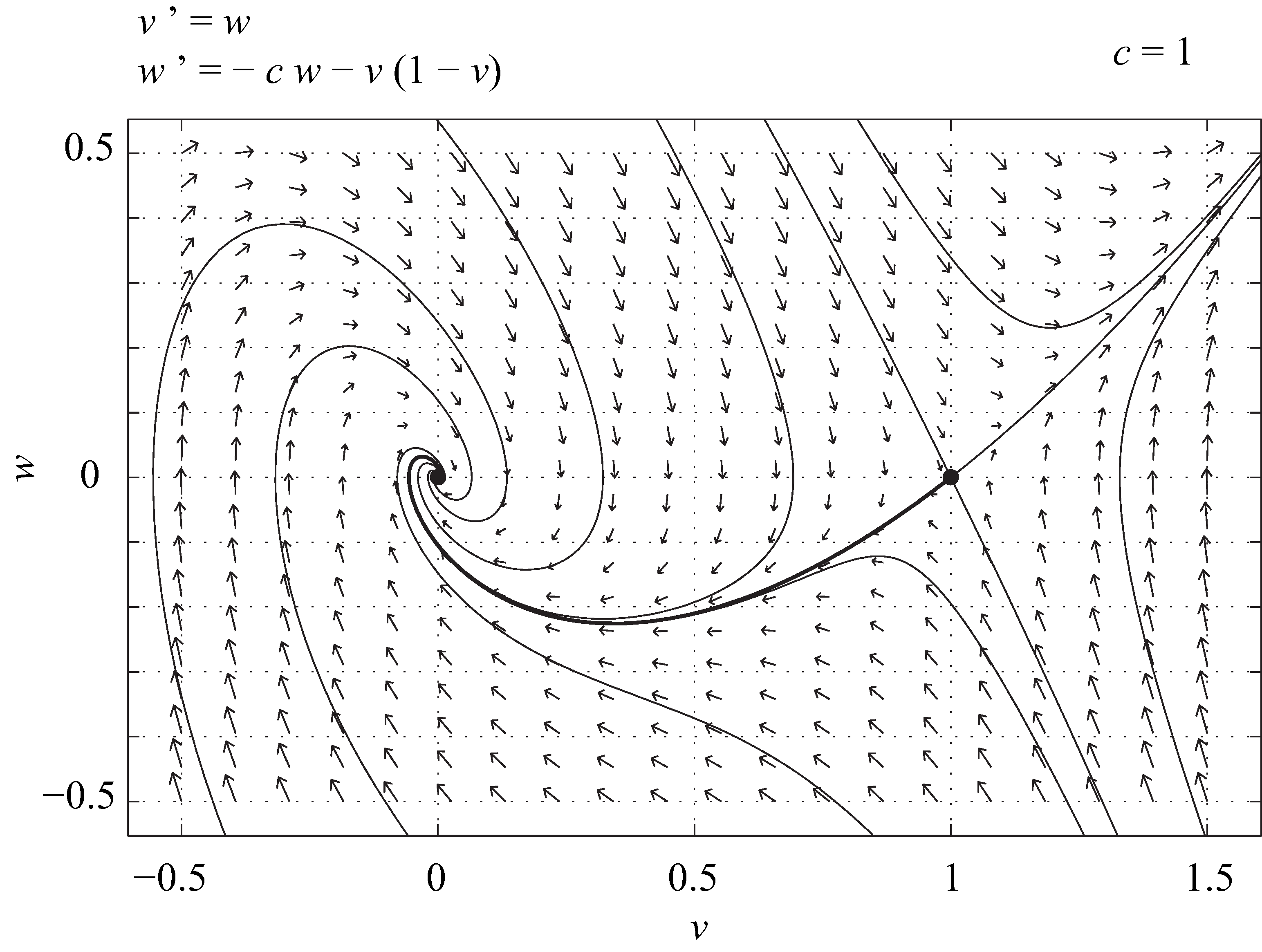
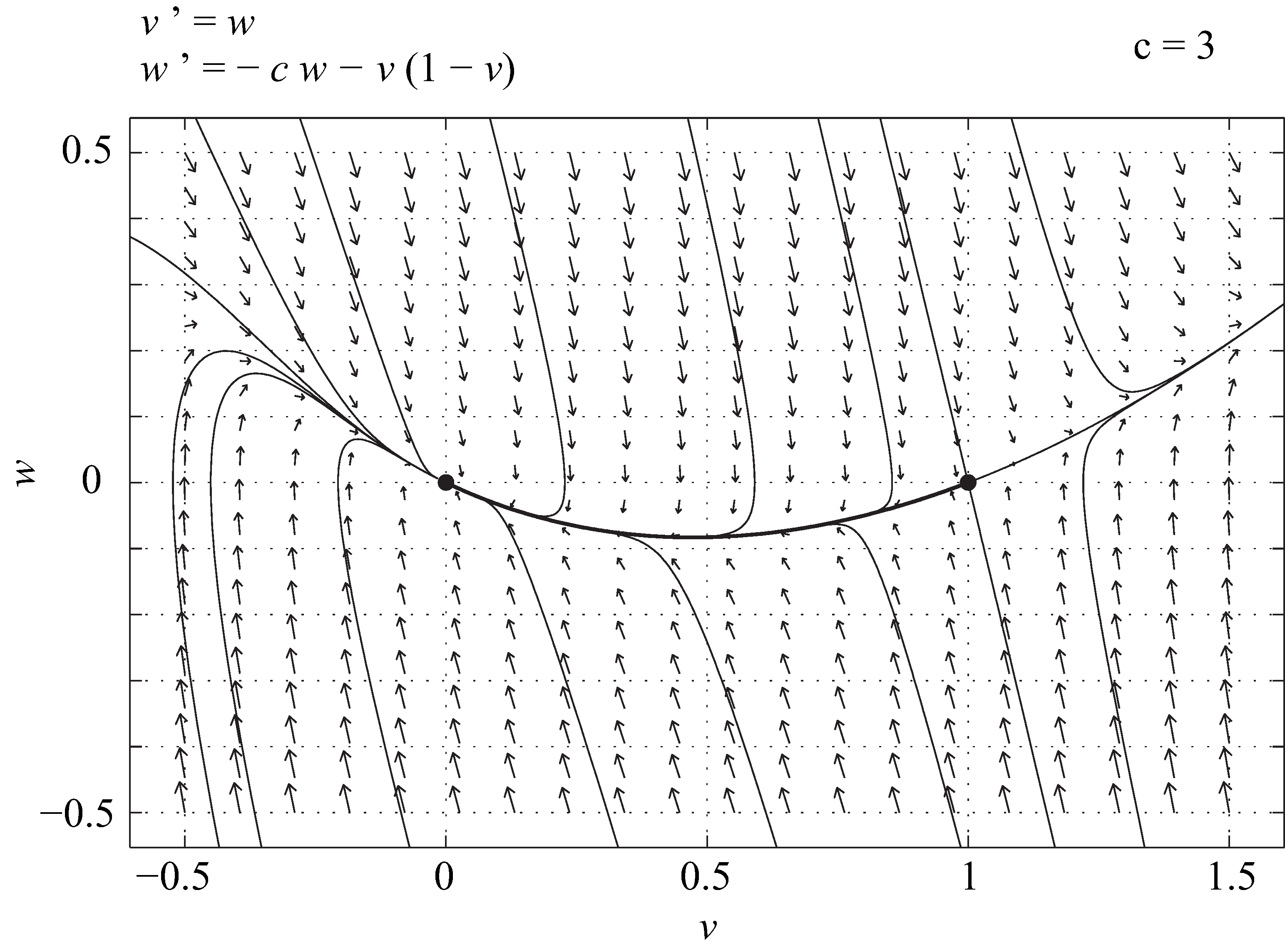
The discriminant of the characteristic polynomial of [latex]J(P_0)[/latex], [latex]c^2 - 4[/latex], is positive for [latex]c > 2[/latex], in which case the origin is a stable node. The front solution is therefore monotonic if [latex]c > 2[/latex], and oscillatory if [latex]0 < c < 2.[/latex] Figures 9.2 and 9.3 show the phase portraits of (9.10), for [latex]c = 1[/latex] and [latex]c = 3[/latex] respectively. In both cases, the front corresponds to the heteroclinic connection between [latex]P_1[/latex] and [latex]P_0[/latex], which is plotted as a thick solid line. If [latex]n[/latex] describes a population density, it cannot become negative, and only speeds larger than [latex]2[/latex] are thus possible. There is nevertheless a whole family of fronts, only one of which is selected by the partial differential equation (9.8).
Chemical waves
When a chemical reaction takes place in a spatially extended system, diffusion should be taken into account. As a consequence, the rate equations discussed in Chapter 8 are turned into partial differential equations. The reaction terms remain the same, but the concentration of each chemical now diffuses with a diffusion coefficient which depends on the size and weight of the molecule in question. If the reaction is oscillatory, wave fronts, corresponding to say large concentrations of some chemical, propagate in the system. Moreover, if the reaction is constrained to a two-dimensional surface and the wave is initiated at some point in space, then the wave fronts are circular. A 2001 article by C. Sachs et al.[4] describes how such wave fronts are observed in an experiment, and proposes a reaction-diffusion model which reproduces this behavior. The authors also discuss the limitation of reaction-diffusion models when macroscopic parameters are affected by the details of microscopic interactions.
What would happen if the wave front was broken, for instance if the wave went over a region where the reaction could not take place? If the wave front is anchored at one point, then it will curve and eventually form a spiral wave. Such waves are often observed in experiments where the Belousov-Zhabotinsky reaction is constrained to a two-dimensional surface, such as a thin film, a porous glass disk, or even a sheet of filter paper. For more information, the reader is referred to the original article by S.C. Müller et al.[5], which discusses experiments revealing the structure of the core of such spiral waves.
Summary
Reaction-diffusion equations extend ordinary differential equation models to entire spatial areas in one, two, or three dimensions. At the macroscopic level, diffusion describe the tendency of a quantity to spread out, by moving in a direction opposite to its local gradient. At the microscopic level, diffusion is associated with an isotropic random walk. Some reaction-diffusion equations admit traveling wave solutions, which may be found by means of dynamical systems methods.
Food for thought
Problem 1
Describe the behavior of system (9.10) near the origin if [latex]c = 2[/latex].
Problem 2
Consider the function
[latex]\displaystyle f(x,t) = \frac{1}{2 \sqrt{\pi D_0 t}} \int_{-\infty}^\infty \exp\left[-\frac{(x-x_0)^2}{4 D_0 t}\right] H(x_0)\ dx_0.[/latex]
- Calculate [latex]\partial f / \partial t[/latex].
- Calculate [latex]\partial^2 f / \partial x^2[/latex].
- Show that [latex]f[/latex] solves the differential equation
[latex]\displaystyle \frac{\partial f}{\partial t} = D_0 \frac{\partial^2 f}{\partial x^2}.[/latex]
Problem 3
Consider a collection of bacteria, which are chemotactic to food. This means that at the macroscopic level, the flow [latex]\vec \jmath[/latex] of bacteria is given by
[latex]\vec \jmath = \chi \vec \nabla n - D \vec \nabla b,[/latex]
where [latex]n[/latex] is the concentration of nutrients, [latex]b[/latex] the density of bacteria, [latex]D[/latex] a diffusion coefficient, and [latex]\chi[/latex] is a chemotactic coefficient.
Write a simple reaction-diffusion model for [latex]n[/latex] and [latex]b[/latex], which takes into account bacterial motion, the diffusion of nutrients, and the fact that bacteria multiply by eating nutrients.
Problem 4
Consider the chemotactic bacteria described in Problem 3. Describe how you would modify the random motion of each bacterium at the microscopic level in order to include chemotaxis.
Problem 5
Consider a particle performing a one-dimensional random walk, such that its probability of taking a step to the right (resp. to the left) is [latex]p[/latex] (resp. [latex]1-p[/latex]), with [latex]p[/latex] not necessarily equal to 1/2. Describe how far you expect the particle to have moved after [latex]N[/latex] steps.
Problem 6
Consider the heteroclinic trajectory of Figure 9.2. Sketch the graph of [latex]v[/latex] as a function of [latex]\xi[/latex]. Explain why such a function cannot represent a population density.
Problem 7
Consider the heteroclinic trajectory of Figure 9.3. Sketch the graph of [latex]v[/latex] as a function of [latex]\xi[/latex].
- R.A. Fisher, The wave of advance of advantageous genes, Annu. Eugenics 7, 255-369 (1937). Statement from the publisher, with which this author agrees: "The work of eugenicists was often pervaded by prejudice against racial, ethnic and disabled groups. Publication of this material online is for scholarly research purposes is not an endorsement or promotion of the views expressed in any of these articles or eugenics in general." ↵
- A. Kolmogorov, I. Petrovsky, N. Piscounoff, Study of the diffusion equation with growth of the quantity of matter and its application to a biology problem, Bulletin de l'Université d'état à Moscou, Ser. int., Section A, Vol. 1 (1937); translated in P. Pelcé, Dynamics of curved fronts, Academic Press, San Diego, 1988. ↵
- For a review, see for instance W. van Saarloos, Front propagation into unstable states, Physics Reports 386, 29-222 (2003). ↵
- C. Sachs, M. Hildebrand, S. Völkening, J. Wintterlin, G. Ertl, Spatiotemporal self-organization in a surface reaction: from the atomic to the mesoscopic scale, Science 293, 1635-1638 (2001). ↵
- S.C. Müller, T. Plesser and B. Hess, The structure of the core of the spiral wave in the Belousov-Zhabotinskii reaction, Science 230, 661-663 (1985). ↵

