We will start our exploration of mathematical modeling with a simple problem, which does not require any particular a priori knowledge, but which allows us to illustrate the modeling process discussed in the previous chapter.

Formulation of the problem

We will consider the problem of the human wave, which occurs in a stadium when spectators stand up, raise their hands and sit down, in order to form a wave which propagates around the bleachers. According to Farkas et al., such a phenomenon is often called the Mexican Wave (La Ola), a term that was first used during the broadcasting of the 1986 Soccer World Cup held in Mexico. The discussion below is based on two articles by Farkas et al. entitled Mexican waves in an excitable medium and Human waves in stadiums.

Our goal is to develop a model that reproduces and explains the propagation of the wave. The model will have to depend on parameters that can be described in everyday terms, and the behavior of the model when these parameters are changed should correspond to what is actually observed in a stadium.

Obtain data and choose the level of complexity of the model

The two articles by Farkas et al. referenced above provide some information, based on 14 video recordings of waves in stadiums containing more than 50,000 seats. Their observations indicate that waves propagate on average at a speed of 12 m s^-1 (or equivalently 22 seats per second), and have a width between 6 and 12 meters (or equivalently 11 to 22 seats), with an average of about 15 seats. Moreover, approximately 3 out of 4 waves propagate clockwise, when one looks at the stadium from above.

Our model will be as simple as possible. In particular, it will be  one-dimensional, and discrete. We will however carefully define our hypotheses so that we will know what to modify if other effects need to be included.

Make assumptions

We will use periodic boundary conditions, since each row in a stadium forms a closed loop. We will not take into account the presence of stairs, and thus assume that all of the seats are equally spaced. We will also consider that all seats are occupied. Each spectator will be either seated or doing the wave. This latter state corresponds to consecutively standing up, waving one’s hands, and sitting down. Once a person has started doing the wave, they will not stop until they are seated again. At that time, the person may decide to stand up and do the wave again.

Set up the model

First, the wave needs to be initiated: some people must be standing up for the wave to start. Then, for the wave to propagate, spectators must be influenced by what their neighbors do. Since most waves propagate in a clockwise direction, people must be more sensitive to what is happening on their right than on their left.

It is clear that the mood of the spectators is important: if the game is too boring, no one will feel like cheering. On the other hand, if the game is too exciting, there may be people standing up all the time, and many waves could be initiated at once. Based on this, we can describe the wave as a wave of enthusiasm. People standing up are excited and their behavior influences the level of enthusiasm of their neighbors. If this level is above a person’s threshold of enthusiasm, then the person will become excited and start doing the wave as well.

We will therefore need a parameter, [latex]s_{th}[/latex], that describes the mood, or the threshold of enthusiasm, of each spectator. This parameter is likely to vary from one spectator to the next, and we will simply assume that it is uniformly distributed over an interval [latex][c - \delta, c + \delta][/latex]. More complicated distributions could be used. The parameter [latex]c[/latex] describes the average responsiveness of the crowd watching the game, and [latex]\delta / \sqrt 3[/latex] measures the spread or the standard deviation of this responsiveness about its mean.

We will assume that a person’s level of enthusiasm varies as they do the wave. This is reasonable since it seems legitimate to consider that a person who is standing and waving is more excited than a person who is just getting up or sitting down. We will thus introduce a function [latex]f(t)[/latex] that describes the level of enthusiasm of a person doing the wave, as a function of time.

Finally, we will define an asymmetric function, [latex]w[/latex] which describes how a spectator is influenced by the behavior – in our case the level of enthusiasm – of their neighbors. We now discuss how to convert the above statements into equations.

Let [latex]N[/latex] be the number of seats in one row of the stadium (recall that this is a one-dimensional model. It can however easily be extended to two dimensions, as is the case for the models discussed in the articles by Farkas et al.). Since we assumed that all seats are occupied, we can define a function [latex]x(i)[/latex] describing the level of enthusiasm of spectator [latex]i[/latex], for [latex]i = 1 \cdots N[/latex]. The variable [latex]x[/latex] will be either 0, if the person is seated, or larger than some activity threshold [latex]\mathcal A[/latex]. If [latex]x(i)=0[/latex], then spectator [latex]i[/latex] will start doing the wave only if the combined enthusiasm of their neighbors, denoted by [latex]w(i)[/latex], exceeds [latex]s_{th}(i)[/latex], i.e. exceeds their threshold of enthusiasm. Once [latex]x(i)[/latex] becomes non-zero, this variable will evolve as a function of time as follows:

[latex]x(i,t) = \left\{ \begin{array}{ll} f(t) & \qquad \hbox{if } f(t) > {\mathcal A} \\ 0 & \qquad \hbox{if } f(t) \le {\mathcal A} \end{array} \right. . \qquad (2.1)[/latex]

The function [latex]f(t)[/latex] should be bell-shaped, its maximum corresponding to the moment when the person is standing up with their hands up. Many functional forms can be chosen; here, we will simply take [latex]f(t) = 1 / \cosh(b (t - t_0)),[/latex] where [latex]t_0[/latex] is the maximizer of [latex]f[/latex] and [latex]b[/latex] is a parameter which selects the duration [latex]\tau[/latex] of the wave, that is how long it takes for one person to stand up, raise their hands, and sit down. More precisely, since the function [latex]1/\cosh(t)[/latex] is of order one on an interval centered at the origin and of width [latex]10[/latex], [latex]\tau[/latex] can be approximated by

[latex]\tau \simeq \frac{10}{b}.[/latex]

We will choose [latex]t_0[/latex] such that [latex]t_0 = t_{\mathcal I} + \Delta \tau,[/latex] where [latex]t_{\mathcal I}[/latex] is the time at which a person becomes excited, i.e. at which [latex]w(i)[/latex] exceeds [latex]s_{th}(i)[/latex], and [latex]\Delta \tau[/latex] is a parameter that we can adjust. One can think of [latex]\Delta \tau[/latex] as a reaction time, which measures the time elapsed between the moment a person notices their neighbors’ activity and the moment they stand up and do the wave.

Since observation of human waves indicate that most waves propagate clockwise, we will use an asymmetric function to describe the combined level of enthusiasm of a person’s neighbors. Again, many choices are possible. Here, we use

[latex]w(i) = \sum_{\begin{array}{c}j,\ |i-j| \le R_m \\ x(j) > {\mathcal A} \end{array}} e^{-|i-j|/R}\ \left(1 - \tanh(a (j-i))\right),[/latex]

where [latex]a[/latex], [latex]R[/latex] and [latex]R_m[/latex] are parameters. This function is such that spectator [latex]i[/latex] is affected by excited neighbors seating less than [latex]R_m+1[/latex] seats away. The exponential term indicates that the most important influence comes from nearest neighbors, and the hyperbolic tangent term is such that neighbors on the right of person [latex]i[/latex] are more influential than neighbors on the left (for positive values of [latex]a[/latex]). When looking at the one-dimensional row from the center of the stadium, the more influential neighbors are thus seated left of person [latex]i[/latex], leading to a wave propagating clockwise.

Test the model

The best way to test this model is by numerical simulation. Once we have chosen the number of seats, the number of people initially standing and the enthusiasm threshold of each of the spectators, and we have defined the functions [latex]f[/latex] and [latex]w[/latex], we can iteratively apply the rule given by Equation (2.1) to each spectator. Whether the wave propagates or dies will depend on the parameters of the model, and we can explore different situations by changing these parameters.

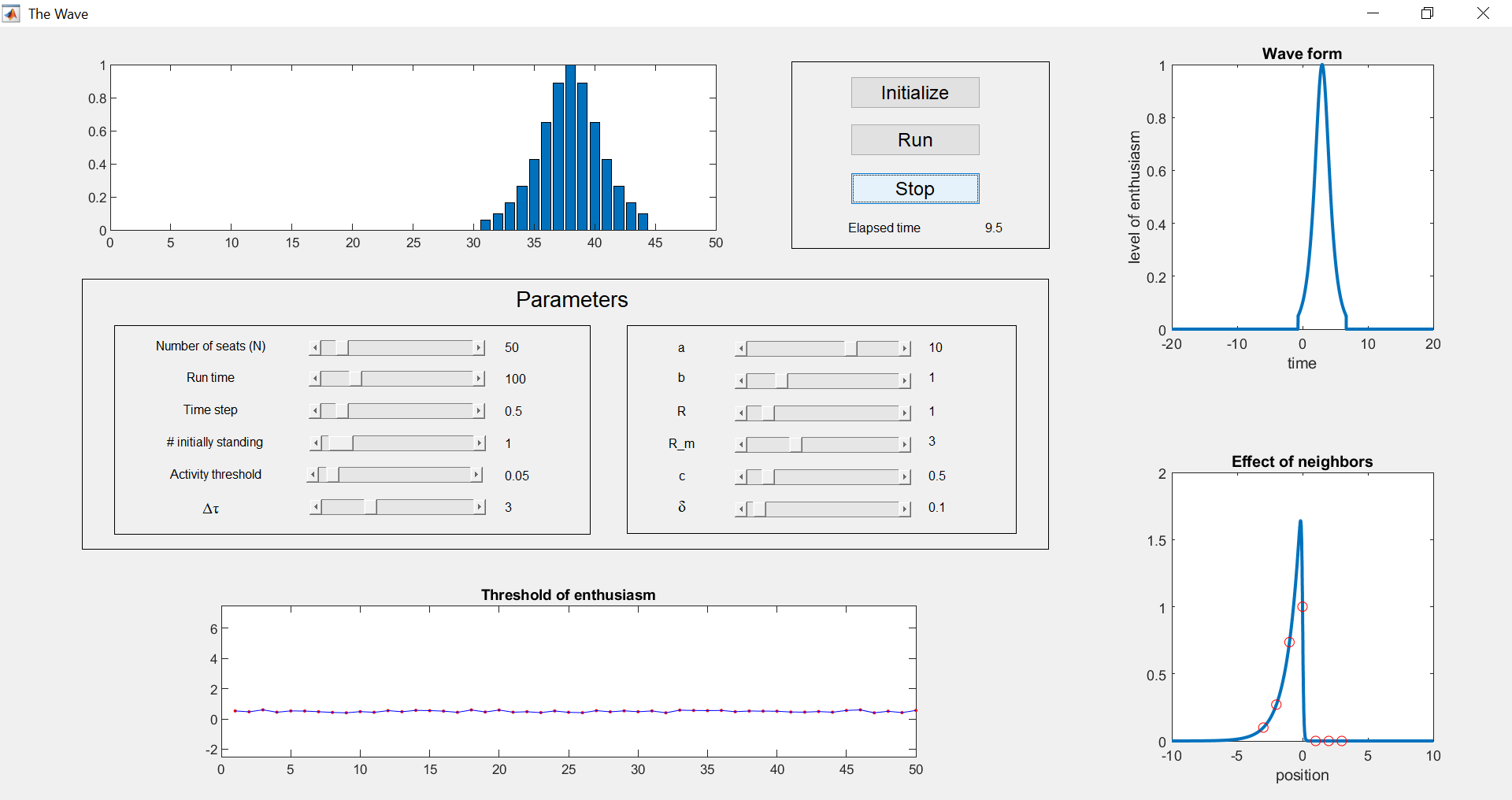
The MATLAB code The_Wave.m simulates the above model. Figure 2.1 shows the corresponding MATLAB interface. The various parameters may be modified by adjusting sliders. When the simulation runs, a plot of [latex]x(i)[/latex] is shown in the top left window, and is updated every time step, [latex]t_r[/latex]. The bottom left window displays a spectator’s threshold of enthusiasm, [latex]s_{th}(i),[/latex] as a function of their seat number [latex]i[/latex]. The top right panel shows the graph, as a function of [latex]t[/latex], of the level of enthusiasm [latex]x(i,t)[/latex] (see Equation (2.1)) of a person doing the wave. The bottom right panel illustrates how neighbors affect the behavior of a person. More precisely, it shows the graph of

[latex]e^{-|i-j|/R}\ \left(1 - \tanh(a (j-i))\right)[/latex]

as a function of [latex]j-i[/latex]; the red circles indicate the contribution of spectator [latex]j[/latex] sitting within a distance [latex]R_m[/latex] of spectator [latex]i[/latex]. All of these windows are updated when the parameters are changed by the user. Default parameter values are such that a wave about 15 seats wide propagates clockwise. Below are a few suggestions for exploring the model.

• Change the number of seats and check that the size of the wave is not affected, provided [latex]N[/latex] is larger than the width [latex]\mathcal W[/latex] of the wave. What happens if [latex]N[/latex] is less than [latex]\mathcal W[/latex]?
• Change the threshold of enthusiasm of the spectators, by modifying the mean [latex]c[/latex] and the range [latex][c - \delta, c + \delta][/latex] of [latex]s_{th}[/latex].
• Change the values of [latex]R[/latex] and [latex]R_m[/latex]. What do you observe?
• Is there a relation between the minimum value of [latex]c[/latex] and the minimum value of [latex]R[/latex] for a wave to form? Why or why not? What is the significance of such a relation?
• What is the speed of the wave?
• Change the time step [latex]t_r[/latex]. How does it affect the size of the wave? Can you modify the value of [latex]b[/latex] to compensate? Why or why not? (Hint: what other time scale is there in the model?) What does [latex]t_r[/latex] actually select? Why?
• Change the activity threshold [latex]\mathcal A[/latex]. Do you understand why the wave dies when [latex]\mathcal A[/latex] is too large? What other parameter can you modify to prevent this from happening?
• Change the number of people initially standing. What do you observe?
• What can you change to make the wave propagate to the left (i.e. anti-clockwise)?

The above numerical exploration shows that the model gives a reasonable representation of the formation and propagation of a wave in a stadium. But the simulation can also help identify some of the limitations of the model. For instance, stairs or aisles could block the propagation of the wave. Another limitation is that if there is more than one person initially standing up, all of these spectators sit down in exactly the same fashion. This is because we use the same function [latex]f(t)[/latex] for each spectator. In practice, different people do the wave differently, and one could think of letting the function [latex]f[/latex] depend on [latex]i[/latex].

Even the simple version of the model presented here has a large number of parameters. A numerical exploration of the model indicates that it is not the parameters themselves, but combinations thereof, which are in fact relevant. For instance, we could decide to measure time in units of the time step, [latex]t_r[/latex]. Then, we would be left with only two dimensionless parameters, [latex]\tau/t_r[/latex] and [latex]\Delta \tau/t_r[/latex]. Identifying relevant combinations of parameters is essential for a thorough exploration of the properties of any model. We will discuss this at length in the next chapter, when we introduce dimensional analysis and scalings.

Summary

This chapter illustrates the various steps involved in the modeling process, using the example of a human wave in a stadium. These steps consist in formulating the problem, obtaining data, identifying the level of complexity of the desired model, making simplifying assumptions, setting up the model and finally testing it. The tools we used were elements of calculus, to choose the functional forms of [latex]f[/latex] and [latex]w[/latex], and numerical simulation. The latter helped us test the model, but simulations are also useful to build an intuitive understanding of the properties of any model. This knowledge can then be used to identify the ingredients responsible for each particular property of a model, and possibly simplify or modify the model accordingly. The phenomenon discussed in this chapter is an example of wave propagation in an excitable medium.

A system is said to be excitable if perturbations of large enough amplitude can trigger a fast and large response, followed by a slower relaxation of the system back to its resting state. Other examples of excitable media include neurons (nerve impulses are excitable waves – called action potentials – propagating along axons) and cardiac tissue (a heartbeat corresponds to an electric wave propagating through the heart, leading to contraction and relaxation of the heart muscle).