We now consider the problem of modeling stone-skipping. The goal is to understand how the stone skims the surface of the water and how far it goes. With this information, it should be possible to suggest an optimal way of throwing the stone, in order to increase the number of rebounds. One of the major differences with the problem of the pendulum discussed previously, is that the stone cannot be considered as a point mass. As a consequence, we will use two sets of model equations: the conservation of momentum to describe the motion of the center of mass (a point), and the equations of motion for a rigid body, to describe the rotation of the stone about its center of mass.

Experimental data

We probably all have some sort of experience with stone-skipping, and we intuitively know that in order to get a large number of bounces, the stone should be rather flat, and thrown with a small incidence angle, and with a spin. We also know that if we do not throw the stone correctly, it may bounce once, but will then start tumbling while in the air and then sink. Remarkably enough, controlled experimental data is available for this problem. A 2004 article^[1] by C. Clanet, F. Hersen and L. Bocquet reports laboratory measurements giving the minimal initial velocity of the stone, the angle between the velocity vector of the stone and the water surface, as well as the collision time, as functions of the angle between the stone and the water surface.

Assumptions and model equations

The discussion below is based on the 2003 article^[2] by L. Bocquet, entitled The physics of stone skipping. We use the same notation, in order to make the reading easier.

We will assume that the motion of the stone alternates between free flight, when the stone is in the air, and collisions with the surface of the water. Each of these stages can be described separately, using equations of classical mechanics. The initial conditions for say a free flight phase will be the position and velocity of the stone as it takes off from the water at the end of the preceding collision phase, and vice-versa. We will start by describing the collision process, and then discuss the free flight part of the motion.

Collision phase

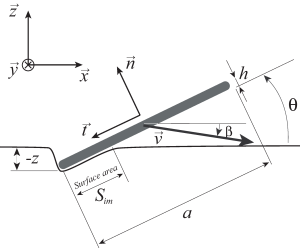
Consider a thin, flat (planar), homogeneous and symmetric (e.g. square or circular) stone of total mass [latex]M[/latex] and assume that during the collision process, the stone does not spin or tumble, and thus remains parallel to itself.^[3] As a consequence, the problem may be simplified by considering the cross-section of the stone through its center of mass and parallel to the plane defined by the vertical and the velocity vector of the stone (see Figure 4.1). All of the points in this cross-section (and in fact in the stone) thus move with the same velocity vector.

The parameters for this problem are then the size [latex]a[/latex] of the stone ([latex]a[/latex] is the side length of a square stone or the diameter of a circular stone), its thickness [latex]h \ll a[/latex], its velocity vector [latex]\vec v(t)[/latex], and the angle [latex]\theta[/latex] (assumed constant during each collision phase) made by the stone with the surface of the water. We will call [latex]\beta(t)[/latex] the angle between [latex]\vec v(t)[/latex] and the horizontal, and define two orthonormal bases: [latex](\vec x, \vec y, \vec z)[/latex] and [latex](\vec n, \vec y, \vec t)[/latex], such that [latex]\vec y[/latex] is perpendicular to the plane of the cross-section, [latex]\vec z[/latex] points upward, [latex]\vec n[/latex] is normal and [latex]\vec t[/latex] is tangent to the surface of the stone. See Figure 4.1 for an illustration.

Since we made the assumption that the stone does not rotate during the collision process, its motion can be reduced to that of its center of mass, and is completely described by Newton’s law. The forces applied to the stone are the force of gravity, [latex]- M g\, \vec z[/latex], and the force [latex]\vec F = F_x\, \vec x + F_z\, \vec z[/latex] exerted by the water on the stone. If we write [latex]\vec v = v_x\, \vec x + v_z\, \vec z[/latex], we have

[latex]M\ \frac{d v_x}{d t} = F_x, \qquad M\ \frac{d v_z}{d t} = - M g + F_z. \qquad (4.1)[/latex]

Of course, we now need a model for the force [latex]\vec F[/latex]. First, this force can be considered as being the sum of a lift force, parallel to [latex]\vec n[/latex], and of a friction force, parallel to [latex]\vec t[/latex]. Second, let us consider the dynamic of the water during the collision process. The fluid moves according to the Navier-Stokes equation,

[latex]\displaystyle \rho_w \left( \frac{d \vec V}{d t} + \left(\vec V \cdot \vec \nabla \right) \vec V \right)= - \nabla p + \mu \nabla^2 \vec V + \vec f,[/latex]

where [latex]\rho_w[/latex] is the density of the water, [latex]\vec V[/latex] is the velocity vector of a fluid particle, [latex]p[/latex] is the pressure, [latex]\mu[/latex] is the dynamic viscosity of the water, and [latex]\vec f[/latex] represents bulk forces (such as gravity) exerted on the water. At the interface between the water and the stone, the pressure [latex]p[/latex] is given by

[latex]\displaystyle p \simeq \frac{||\vec F||}{S_{im}},[/latex]

where [latex]S_{im}[/latex] is the surface area of the immersed portion of the stone (see Figure 4.1). We will now perform some dimensional analysis to compare the inertial and diffusive terms in this equation. We have

[latex]\displaystyle \frac{\left[ \rho_w \left( \vec V \cdot \vec \nabla\right) \vec V \right]}{\left[\mu \vec \nabla^2 \vec V\right]} = \left[ \frac{\rho_w ||\vec V|| L}{\mu} \right] = \left[ \frac{||\vec V|| L}{\nu_w} \right] \equiv Re,[/latex]

where [latex]L[/latex] is a characteristic length, [latex]\nu_w = \mu / \rho_w[/latex] is the kinematic viscosity of water, and [latex]Re[/latex] is called the Reynolds number. If we assume that [latex]||\vec V||[/latex] is of the order of a few meters per second, that [latex]L[/latex] is of the order of the size of the stone – say a few centimeters – and since, for water, [latex]\nu_w = 10^{-6}[/latex] m² s[latex]^{-1}[/latex], we find

[latex]Re = \frac{10 \cdot 10^{-2}}{10^{-6}} = 10^5 \gg 1.[/latex]

As a consequence, viscous terms are negligible, and we can balance inertial terms with pressure terms. This gives

[latex]\left[ \frac{p}{L} \right] \simeq \left[ \rho_w \left( \vec V \cdot \vec \nabla\right) \vec V \right] = \left[ \frac{\rho_w ||\vec V||^2}{L} \right],[/latex]

which together with [latex]p \simeq ||\vec F||/S_{im}[/latex] gives

[latex]||\vec F|| \propto \rho_w\, S_{im}\, ||\vec V||^2.[/latex]

Since [latex]||\vec V||[/latex] and [latex]||\vec v||[/latex] are comparable, we will thus consider that the intensity of the force [latex]\vec F[/latex] is proportional to the density of water [latex]\rho_w[/latex], the immersed surface area [latex]S_{im}[/latex], and the square of the velocity vector of the stone, [latex]||\vec v||^2[/latex]. We can then write

[latex]\vec F = \left(\frac{1}{2} C_l\, \vec n + \frac{1}{2} C_f \, \vec t \right) \rho_w \, S_{im} \left(v_x^2 + v_z^2\right),[/latex]

where the dimensionless coefficients [latex]C_l[/latex] and [latex]C_f[/latex] describe how the normal (lift) and tangential (friction) components of [latex]\vec F[/latex] vary with [latex]\rho_w \, S_{im}\, ||\vec v||^2[/latex]. We will assume that these coefficients are constant. We can now substitute this expression into Equations (4.1). Since [latex]\vec n = - \sin(\theta) \, \vec x + \cos(\theta)\, \vec z[/latex] and [latex]\vec t = - \cos(\theta)\, \vec x - \sin(\theta) \vec z[/latex], we get

[latex]\begin{array}{ll} \displaystyle M\ \frac{d v_x}{d t} = - \frac{1}{2} \rho_w \, S_{im}(z) \left(v_x^2 + v_z^2\right) \left(C_l \sin(\theta) + C_f \cos(\theta)\right),\\ \displaystyle M \ \frac{d v_z}{d t} = - M g + \frac{1}{2} \rho_w \, S_{im}(z) \left(v_x^2 + v_z^2\right) \left(C_l \cos(\theta) - C_f \sin(\theta)\right). \end{array}\qquad(4.2)[/latex]

These equations are nonlinear in [latex]v_x[/latex] and [latex]v_z[/latex]. Moreover, we made explicit the dependence of [latex]S_{im}[/latex] on the vertical coordinate [latex]z[/latex] of the part of the stone that is the deepest under water (see Figure 4.1). Equations (4.2) are valid as long as the stone is not completely immersed. If this happened, the lift exerted by the water on the stone would be given by Archimedes’ law, and the stone would sink. At the beginning of the collision phase, [latex]v_z < 0[/latex]. In order for the stone to skim the surface of the water, we need to have [latex]d v_z / d t > 0[/latex], so that [latex]v_z[/latex] is positive at the end of the collision phase. We see that the angle [latex]\theta[/latex] needs to be small for this to happen, since [latex]C_l \cos(\theta) - C_f \sin(\theta)[/latex] must be positive if we want

[latex]\frac{1}{2} \rho_w \, S_{im}(z) \left(v_x^2 + v_z^2\right) \left(C_l \cos(\theta) - C_f \sin(\theta)\right)[/latex]

to balance [latex]- M g[/latex].

Free flight phase

During a free flight phase, the motion of the center of mass of the stone is described by Newton’s equation in which the only force is gravity:

[latex]\displaystyle M\ \frac{d v_x}{d t} = 0, \qquad M\ \frac{d v_z}{d t}= - M g. \qquad (4.3)[/latex]

If we denote by [latex]X[/latex] and [latex]Z[/latex] the coordinates of the stone, we have

[latex]X(t)=X(0) + v_x(0) t \qquad Z(t) = v_z(0) t -\frac{1}{2} g t^2, \qquad (4.4)[/latex]

where [latex]t=0[/latex] is taken at the beginning of the free flight phase. The initial position [latex](X(0), Z(0)=0)[/latex] and velocity [latex](v_x(0),v_z(0))[/latex] of the stone are given by the final position and velocities of the preceding collision phase, unless of course this is the first free flight phase.

The rigid rotation of the stone about its center of mass is given by Euler’s equations,

[latex]\begin{array}{ll}&I_{-y} \displaystyle \frac{d \omega_y}{d t} - \omega_n \omega_p (I_n - I_p) = N_{-y}\\& \displaystyle I_n \frac{d \omega_n}{d t} - \omega_p \omega_{-y} (I_p - I_{-y}) = N_n \\ & \displaystyle I_t \frac{d \omega_p}{d t} - \omega_{-y} \omega_n (I_{-y} - I_n) = N_p,\end{array} \qquad (4.5)[/latex]

where [latex]I_\alpha[/latex], [latex]\omega_\alpha[/latex] and [latex]N_\alpha[/latex] are respectively the moment of inertia, angular frequency and torque about the body principal axis parallel to [latex]\vec \alpha[/latex]. Here, [latex]-\vec y[/latex] and [latex]\vec p[/latex] are unit vectors tangent to the surface of the stone, and parallel to two of its principal axes. The orthonormal frame [latex](-\vec y, \vec n, \vec p)[/latex] is attached to the center of mass of the stone, and rotates with it. A similar set of equations could be written for the collision phase of the motion, if we wanted to take into account the fact that the stone may be spinning and tumbling as it collides with the water.

Since the stone is square or circular, one has [latex]I_{-y} = I_p \equiv J_1[/latex], and we will use the notation [latex]I_n \equiv J_0[/latex]. Moreover, the only force acting on the stone, [latex]-M g\, \vec z[/latex], is applied at its center of mass, so that all of the torques are zero. Equations (4.5) can then be simplified into

[latex]\begin{array}{ll}& J_1 \displaystyle \frac{d \omega_{-y}}{d t} - \omega_n \omega_p (J_0 - J_1) = 0 \\ & J_0\, \displaystyle \frac{d \omega_n}{d t} = 0 \\& J_1 \displaystyle \frac{d \omega_p}{d t} - \omega_{-y} \omega_n (J_1 - J_0) =0. \end{array} \qquad (4.6)[/latex]

Analysis

We will start by analyzing the equations for the free flight phase of the motion, and then go back to the collision process.

Free flight phase

From Equations (4.6), we see that [latex]\omega_n[/latex] is conserved, and is thus equal to the initial spinning velocity [latex]\Omega_0[/latex] of the stone about the axis normal to its surface and through its center of mass. We are thus left with two linear equations,

 [latex]\begin{array} \displaystyle J_1 \frac{d \omega_{-y}}{d t} - \Omega_0\, \omega_p (J_0 - J_1) &= 0 \\ \displaystyle J_1 \frac{d \omega_p}{d t} - \omega_{-y}\, \Omega_0 (J_1 - J_0) &= 0, \end{array} \qquad (4.7)[/latex]

which read, in matrix form, [latex]\displaystyle \frac{d}{dt} \left(\begin{array}{c}\omega_{-y} \\ \omega_p \end{array}\right) = \left(\begin{array}{cc} 0 & \delta \\ -\delta & 0 \end{array}\right) \left(\begin{array}{c}\omega_{-y} \\ \omega_p \end{array}\right)[/latex] with [latex]\delta = \frac{\Omega_0 (J_0 -J_1)}{J_1}.[/latex] In the absence of initial spin, i.e. if [latex]\Omega_0 = 0[/latex], we obtain

[latex]\omega_{-y} = \omega_{-y}(0) \qquad \omega_p = \omega_p(0),[/latex]

which implies, since [latex]\omega_{-y}=d \theta/dt[/latex],

[latex]\theta(t) = \omega_{-y}(0)\, t.[/latex]

In other words, if during the collision phase, the stone is even slightly put into rotation about the [latex]\vec y[/latex] axis, i.e. if [latex]\omega_{-y}(0)[/latex] is non-zero, then the stone will start tumbling during the free flight phase. At the next collision, the stone is likely to hit the water with a large incidence angle [latex]\theta[/latex], and then sink.

It is thus critical that [latex]\Omega_0[/latex] be non-zero. In such a case, both [latex]\omega_{-y}[/latex] and [latex]\omega_p[/latex] oscillate in time with frequency [latex]|\delta|[/latex] and are given by

[latex]\begin{array}{c}\omega_{-y}(t) = \omega_{-y}(0) \cos(\delta t) + \omega_p(0) \sin(\delta t) \\ \omega_p(t) = \omega_p(0) \cos(\delta t) - \omega_{-y}(0) \sin(\delta t). \end{array}[/latex]

As a consequence,

[latex]\theta(t) = \theta(0) + \frac{1}{\delta} \omega_{-y}(0) \sin(\delta t) - \frac{1}{\delta} \omega_p(0) \cos(\delta t)[/latex]

and will remain close to [latex]\theta(0)[/latex] if the coefficients of the above equation are small. Thus, a spin about the [latex]\vec n[/latex] direction stabilizes the stone and prevents it from tumbling. This is called the gyroscopic effect.

We now turn to the motion of the center of mass of the stone during a free flight phase. Equations (4.4) tell us that the duration [latex]\tau_f[/latex] of each free flight phase is such that [latex]Z(\tau_f)=0[/latex], i.e.

[latex]\tau_f = \frac{2 v_z(0)}{g},[/latex]

and the length of each skip, that is the distance covered by the stone along the [latex]\vec x[/latex] direction is

[latex]\lambda = v_x(0) \tau_f = v_x(0) \frac{2 v_z(0)}{g}.[/latex]

From Equations (4.2), it is clear that when [latex]\theta[/latex] is small, [latex]v_x[/latex] is decreasing during each collision phase. Thus the value [latex]v_x(0)[/latex] of [latex]v_x[/latex] at the beginning of each free flight phase will decrease from one free flight phase to the next. Since we do not expect [latex]v_z[/latex] to increase between two free flight phases, we see that the length of each skip decreases from one skip to the next, as expected.

Collision phase

Our analysis of Equations (4.2) should first of all indicate under what conditions the stone is going to emerge and take off from the water at the end of a collision phase. Consider the equation for [latex]v_z[/latex],

[latex]M \displaystyle \frac{d v_z}{d t} = - M g + \frac{1}{2} \rho_w \, S_{im}(z) \left(v_x^2 + v_z^2\right) \left(C_l \cos(\theta) - C_f \sin(\theta)\right) . \quad (4.10)[/latex]

We can appreciate the information contained in this equation if we make the approximation [latex]v_x \gg v_z[/latex], which is reasonable, and also assume that [latex]v_x^2 + v_z^2 = v^2 \equiv v_0^2[/latex] is constant during the collision phase. The latter statement is not quite correct since the stone is slowed down by friction with the water, but if the stone bounces about 20 times, then the relative loss [latex](v^2(0) - v^2(\tau_c))/v^2(0)[/latex] during each collision is small, at least for most collisions. Here, [latex]\tau_c[/latex] denotes the duration of the collision. Under these conditions, Equation (4.10) reads

[latex]M \displaystyle \frac{d v_z}{d t} = - M g + \frac{1}{2} \rho_w S_{im}(z) v_0^2 \left(C_l \cos(\theta) - C_f \sin(\theta) \right) \equiv - {\mathcal F}(z). \quad (4.11)[/latex]

The right-hand-side, [latex]- {\mathcal F}(z)[/latex], is a function of [latex]z[/latex] only (recall that we assumed at the beginning that [latex]\theta[/latex] is constant during each collision phase), and since [latex]v_z = d z / d t[/latex], we can multiply both sides of this equation by [latex]v_z[/latex] and integrate with respect to [latex]t[/latex], to get

[latex]\displaystyle \frac{M}{2} \left(\frac{d z}{d t}\right)^2 = \int - {\mathcal F}(z) \frac{d z}{d t} \, dt = \int - {\mathcal F}(z) \, dz \equiv -\, {\mathcal U}(z) + E, \quad (4.12)[/latex]

where [latex]{\mathcal U}(z) = \int_0^z F(s)\, ds,[/latex] and the constant [latex]E[/latex] is arbitrary. When [latex]z=0[/latex], [latex]S_{im}(z)=0[/latex]; moreover, [latex]S_{im}(z)[/latex] increases as [latex]z[/latex] becomes more negative. Therefore, the potential [latex]{\mathcal U}(z)[/latex] has a shape like that drawn in Figure 4.2 for negative [latex]z[/latex]‘s, provided [latex]\theta[/latex] is small enough.

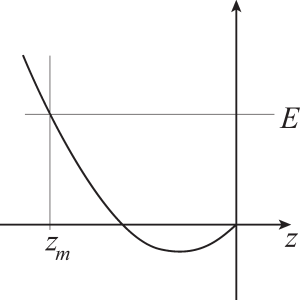
From the shape of [latex]{\mathcal U}[/latex], one can see that the trajectory of the stone will be such that [latex]z[/latex] will have a turning point at [latex]z=z_m[/latex], and that at the end of the collision phase, the stone will emerge with a vertical velocity [latex]v_z(\tau_c) = - v_z(0)[/latex], opposite to the vertical velocity it had at the beginning of the collision phase. This occurs only if the energy [latex]E[/latex] is such that the stone is not completely immersed when [latex]z=z_m[/latex]. If we keep [latex]E[/latex] fixed, this imposes a condition on [latex]v_0^2[/latex] since the larger [latex]v_0^2[/latex], the smaller [latex]|z_m|[/latex]. Therefore, the stone will not sink during a collision phase, provided [latex]v_0^2 > v_c^2[/latex], where the critical velocity [latex]v_c[/latex] depends on the parameters of the problem. Since [latex]v_x \gg v_z[/latex], the condition on [latex]v_0[/latex] can also be re-written as a condition on the initial velocity of the stone in the [latex]\vec x[/latex] direction, which thus reads [latex]v_x(0) > v_c[/latex]. As shown in the 2003 article by L. Bocquet, and in the exercises at the end of this Chapter, one can calculate [latex]S_{im}(z)[/latex] for a stone of a particular shape, solve Equation (4.11) explicitly, and obtain an expression for [latex]v_c[/latex].

As mentioned above, we made the assumption that the dynamics was conservative (i.e. [latex]v^2 = v_0^2[/latex] was assumed constant). This is obviously not true since the stone does not keep bouncing forever. There is a loss of energy during the collision process, due to the friction of the stone on the surface of the water. Everything we said before will be qualitatively correct – in particular the stone will emerge with a vertical velocity only slightly smaller than [latex]|v_z(0)|[/latex] – as long as the relative loss of energy during a collision phase is small. This will certainly be true for the first bounces, but will cease to be valid for the last ones. Since this energy loss is the major reason for the slowing down of the stone, we will now try to estimate this quantity. The (signed) energy loss [latex]\mathcal W[/latex] is equal to the work of the friction force exerted by the water on the stone. This can be roughly estimated as

[latex]\begin{align} {\mathcal W} & \simeq \left[ \text{force along } \vec x \right] \cdot \left[ \text{distance covered by the stone along } \vec x \right] \\ & \simeq \vec F \cdot \vec x l, \end{align}[/latex]

where [latex]l = v_x(0)\ \tau_c[/latex]. From Equation (4.11), we see that

[latex]\left[\frac{\rho_w}{M} v_0^2 \right] = L^{-1} T^{-2},[/latex]

and we can thus expect

[latex]\tau_c \propto \displaystyle \sqrt{\frac{M}{a \rho_w v_0^2}} \simeq \sqrt{\frac{M}{a \rho_w}} \frac{1}{v_x(0)},[/latex]

where [latex]a[/latex] is the size (side length or diameter) of the stone. Therefore, [latex]l = v_x(0) \tau_c[/latex] does not depend on [latex]v_x(0)[/latex] at lowest order. During the collision, the right-hand-side of Equation (4.10) is small, so we can write that

[latex]M g \simeq \vec F \cdot \vec z.[/latex]

Moreover, since

[latex]\displaystyle \frac{\vec F \cdot \vec x}{\vec F \cdot \vec z} = - \frac{C_l \sin(\theta) + C_f \cos(\theta)}{C_l \cos(\theta) - C_f \sin(\theta)} \equiv - \mu,[/latex]

(the ratio [latex]\mu[/latex] should not be confused with the dynamic viscosity of water), we have

[latex]\vec F \cdot \vec x \simeq - M g\, \mu,[/latex]

and

[latex]{\mathcal W} \simeq - M g\, \mu \, l.[/latex]

Thus, since the difference in kinetic energy between the beginning and the end of the collision phase is equal to [latex]\mathcal W[/latex], we have

[latex]\frac{1}{2} M v_x^2(\tau_c) - \frac{1}{2} M v_x^2(0) = {\mathcal W} = - M g\, \mu\, l,[/latex]

and the initial velocity [latex]v_x(0)[/latex] must satisfy

[latex]v_x(0) > \sqrt{2\, g\, \mu\, l} \equiv V_c.[/latex]

Putting everything together, the velocity along [latex]\vec x[/latex] at the beginning of a collision phase must satisfy

[latex]v_x(0) > \max(v_c,V_c),[/latex]

where [latex]v_c[/latex] is obtained by specifying that the stone should not become completely immersed during a collision, and [latex]V_c[/latex] is such that the stone is moving fast enough to compensate for the energy due to friction forces. Our discussion of the free flight phase shows that the length of each jump is proportional to the horizontal velocity [latex]v_x[/latex]. We know that [latex]v_x[/latex] is conserved during a free flight phase (see Equation (4.3)), and that [latex]v_x^2[/latex] decreases by [latex]2\, g\, \mu\, l[/latex] during each collision phase. Since [latex]|v_z|[/latex] is the same at the beginning and end of each free flight phase, and since [latex]v_z[/latex] varies only slightly during a collision phase, the length of a jump after [latex]N[/latex] collision phases will be given by

[latex]\begin{align}\lambda_N &= \frac{2 |v_z(0)|}{g} \sqrt{v_{x,0}^2 - 2 \, N \, g\, \mu\, l} = \frac{2 |v_z(0)| v_{x,0}}{g} \sqrt{1 - \frac{2 \, N \, g\, \mu\, l}{v_{x,0}^2}}\\ &= \lambda_0 \sqrt{1 - \frac{N}{N_c}}, \qquad \lambda_0 = \frac{2 |v_z(0)| v_{x,0}}{g}, \ N_c = \frac{v_{x,0}^2}{2 \, g\, \mu\, l}, \end{align}[/latex]

where [latex]v_{x,0}[/latex] is the [latex]\vec x[/latex]-velocity of the stone as it is initially thrown. We thus see that the length of each jump decreases as [latex]N[/latex] gets large, and scales like [latex]\sqrt{1-N/N_c}[/latex].

Summary

This model explains the existence of a minimum velocity at which the stone should be thrown; it explains why the stone should be given a spin; and it describes how the length of each jump decreases as the number of bounces increases. It also indicate that the angle [latex]\theta[/latex] between the stone and the surface of the water should be small. Experiments described in the article by C. Clanet et al.^[4] show that [latex]\theta = 20^o[/latex] is optimal. This value of [latex]\theta[/latex] minimizes the collision time; it is also the incidence angle for which successful stone-skipping occurs with the smallest initial speed. In order to explain these observations, one would for instance have to take into account the dependence of [latex]C_l[/latex] and [latex]C_n[/latex] on [latex]\theta[/latex], and find the value of [latex]\theta[/latex] that minimizes the energy loss [latex]\mathcal W[/latex].