19 Newton’s Second Law
Let’s remind ourselves of Newton’s first two laws:
Our goal in this chapter is to translate Newton’s second law into math. Let’s start with the opening of Newton’s second law: “When you push or pull an object.” In physics, we refer to a push or a pull as a force. We will use the variable ![]() for “force.” So, if
for “force.” So, if ![]() , we apply a force.
, we apply a force.
Now for the second part: “its velocity will change.” Mathematically, this just means that the object is undergoing acceleration, that is, ![]() . It also makes sense that if
. It also makes sense that if ![]() is big (i.e. a big push), then the change in velocity will be bigger. That is, as
is big (i.e. a big push), then the change in velocity will be bigger. That is, as ![]() gets bigger,
gets bigger, ![]() needs to get bigger.
needs to get bigger.
Exercise 19.1: Relating Force and Acceleration (part I)
What is the simplest possible equation you could write relating force (![]() ) and acceleration (
) and acceleration (![]() ) to ensure that:
) to ensure that:
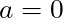 when
when 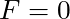
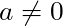 when
when 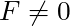 .
.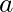 gets bigger when
gets bigger when 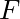 gets bigger?
gets bigger?
We have learned that ![]() , where
, where ![]() is some proportionality constant. This constant is called the mass of the object, and it is different for every object. E.g., when you push a toy car (small
is some proportionality constant. This constant is called the mass of the object, and it is different for every object. E.g., when you push a toy car (small ![]() ), you can get the car going easily (large
), you can get the car going easily (large ![]() ). Push a real car (high
). Push a real car (high ![]() ) with the same force, and the car will hardly start moving (small
) with the same force, and the car will hardly start moving (small ![]() ). This is a rather important point: you may be used to thinking of mass as “the amount of stuff an object has”, or maybe “how heavy the object is.” Neither is correct. As far as physics goes
). This is a rather important point: you may be used to thinking of mass as “the amount of stuff an object has”, or maybe “how heavy the object is.” Neither is correct. As far as physics goes
Mass measures how hard it is to change the velocity of an object.
For this reason, mass can also be thought of as measuring “inertia”, i.e. the resistance of an object to changing its velocity.
Units: in the SI system, mass is measured in units of kilograms, ![]() . This makes the units of force
. This makes the units of force ![]() . This combination of units is called a Newton, denoted by the letter
. This combination of units is called a Newton, denoted by the letter ![]() .
.
For scale, ![]() is roughly the force required to lift an apple.
is roughly the force required to lift an apple.
We’re still not quite done, but we are now very close. We have figured out that forces are vectors, and that ![]() . But- what happens if there is more than one force applied on an object?
. But- what happens if there is more than one force applied on an object?
Exercise 19.2: Newton 2nd Law
Answer the following questions:
Our final conclusion is extremely important. If you have studied physics in the past, you might have learned Newton’s second law as ![]() . This is wrong. The correct way of expressing Newton’s second law is:
. This is wrong. The correct way of expressing Newton’s second law is:
![]() .
.
I urge you to always write Newton’s law in this way. Having graded many exams, I know it’s easy to forget that one must always add up all the forces applied to an object. If you make a point of always writing ![]() , this won’t happen to you.
, this won’t happen to you.
Newton’s law is the single most important equation you will learn this entire semester, so it absolutely goes into our tablets.

Warning: Newton’s 2nd law as written above (i.e. ![]() ) is not quite correct. In particular, it assumes that the mass of an object is constant. If you want to solve problems in which the mass of an object is changing (e.g. a “leaky box” full of sand), then we’ll need a bit more work.
) is not quite correct. In particular, it assumes that the mass of an object is constant. If you want to solve problems in which the mass of an object is changing (e.g. a “leaky box” full of sand), then we’ll need a bit more work.
We will address this caveat in future chapters. For now, though, we will rely on ![]() to keep making progress.
to keep making progress.
Before we set out to solve problems using Newton’s laws, let’s make sure we know how to apply them correctly by considering some conceptual questions.
Exercise 19.3: Using Newton’s Laws
The diagram below shows a box that is being pushed on each of its four sides, as shown. In which direction will the box accelerate? (Click on the appropriate option).
If you’re stuck, you can view my solution below.
Exercise 19.4: Balance the Forces
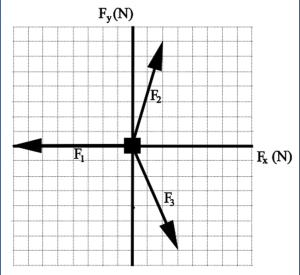
The diagram at right shows a box that is subject to three forces, as shown. You wish to push this box in such a way that the box remains stationary.
What is the force vector you need to apply in order for the box to remain stationary? Each cell is 1 N across.
When an object is subject to multiple forces that all add up to zero, we say the forces are balanced.
The diagrams above are called force diagrams. They help us see what forces are acting on an object, which in turn will allow us to figure out how that object will move in response to those forces. From this point on, all of our drawings need to include force diagrams.
Key Takeaways
