14 Relative Velocity
Suppose you are driving down the highway at 60 mph. We will call your direction of travel the positive direction. You overtake a car traveling at 50 mph. From your point of view, that car is moving backwards, with a velocity of -10 mpg.
Hopefully most of you are comfortable with this scenario. To make this explicit, we write
![]() .
.
We can readily generalize this equation. First, we promote the “velocities” to vectors. Second, this result doesn’t depend on your personal identity, or the fact that it’s a car: it will apply to any observer ![]() , and any other object
, and any other object ![]() , so that
, so that
![]() .
.
In the above equation, the velocities ![]() and
and ![]() are the velocities of
are the velocities of ![]() and
and ![]() as measured by a separate observer, e.g. someone standing on the side of the road. Let’s call this observer
as measured by a separate observer, e.g. someone standing on the side of the road. Let’s call this observer ![]() . You will find it is very useful to use different letters to help keep track of who is doing the measurements. E.g., here, I will use
. You will find it is very useful to use different letters to help keep track of who is doing the measurements. E.g., here, I will use ![]() to denote velocities by our reference observer (observer
to denote velocities by our reference observer (observer ![]() ), and I will let
), and I will let ![]() denote velocities as measured by
denote velocities as measured by ![]() . With this notation, the above equation becomes
. With this notation, the above equation becomes
![]() .
.
In the above equation, the fact that the letter ![]() is used in the left hand side is telling me that
is used in the left hand side is telling me that ![]() is the velocity of
is the velocity of ![]() as measured by
as measured by ![]() . As you will see below, this is very powerful!
. As you will see below, this is very powerful!
Now- the above equation is fully correct, but we didn’t actually derive the equation; we just took the “cars in the highway” equation, and guessed what the final equation would have to look like. Let’s now actually go through the process of deriving the equation. To do so, we will start with a concrete problem.
Exercise 14.1: Relative Velocities
Daniel is standing by the side of road. Daniel’s dog Buster is running parallel to the road at ![]() . Leanna drives by at
. Leanna drives by at ![]() (≈30 mph) in the same direction as Buster is running.
(≈30 mph) in the same direction as Buster is running.
What is Buster’s velocity relative to Leanna?
You might be able to just “see” the answer, but I want us to go slowly over how we can formally solve this problem. This will be useful for when we consider the more general situation below. As usual, we start by drawing a picture (see below). In my drawing, I use the following notation:
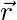 gives positions measured by Daniel
gives positions measured by Daniel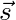 gives positions measured by Leanna
gives positions measured by Leanna
The subscripts of the position vector tell us what the vector is pointing to. For instance, ![]() is the position of Leanna (as measured by Daniel).
is the position of Leanna (as measured by Daniel).
Try labeling my drawing. If you get stuck, you can move the slider to reveal the sketch with my labeling.
On to step 2: find relations. Use the sketch above to find a relation between ![]() ,
, ![]() , and
, and ![]() .
.
Now- we are not really after the relation between positions, but rather the relation between velocities. But velocity is just the derivative of position! All we need to do then is take the derivative of the relation we found. When doing so, I used the following notation:
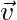 are velocities as measured by Daniel.
are velocities as measured by Daniel.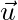 are velocities as measured by Leanna.
are velocities as measured by Leanna.
Again, we can specify whose velocity we are talking about by using a subscript.
Take the derivative with respect to time of the relation between position vectors you derived to find a relation between velocities. Use this relation to determine Buster’s velocity relative to Leanna.
The above problem allowed us to recover the equation we already had, but this time we derived it from first principles. Let’s now go for the most general version of the problem.
Exercise 14.2: Relative Velocities
Consider two observers, Abdul (A) and Bai (B). Abdul measures the velocity of Bai to be ![]() . He also measures the velocity of an object C to be
. He also measures the velocity of an object C to be ![]() We want to figure out the velocity of
We want to figure out the velocity of ![]() as measured by Bai.
as measured by Bai.
Try solving this problem on your own. If you get stuck, I’ll walk you through the solution.
Step 1: Draw a picture. Since the problem doesn’t tell us anything about where ![]() ,
, ![]() , and
, and ![]() are, just draw three points randomly, and label them
are, just draw three points randomly, and label them ![]() ,
, ![]() , and
, and ![]() . Then draw the relevant position vectors.
. Then draw the relevant position vectors.
When labeling your vectors, adopt a similar convention to that of the previous problem:
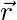 denotes positions as measured by
denotes positions as measured by 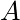 .
.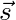 denotes positions as measured by
denotes positions as measured by 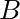 .
.
If you get stuck, my sketch of the solution is shown below; just move the slider to reveal the solution.
Step 2: Find relations. From our sketch, we can derive a simple relation between the vectors ![]() ,
, ![]() , and
, and ![]() . Do so, and then take the derivative with respect to time to find the how the corresponding velocities are related.
. Do so, and then take the derivative with respect to time to find the how the corresponding velocities are related.
Use the following notation:
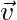 are velocities as measured by
are velocities as measured by 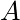 .
.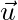 are velocities as measured by
are velocities as measured by 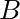 .
.
Step 3: Solve unknowns. Use your result to express the velocity ![]() of object
of object ![]() as measured by Bai in terms of velocities measured by Abdul.
as measured by Bai in terms of velocities measured by Abdul.
The result you derived above is called the Galilean transformation:
![]() .
.
Of course, this is just the equation we wrote down at the very beginning, but we have now formally derived it, so we know it’s always![]() true.
true.
![]() Not always! You might have heard that “nothing can move faster than light.” As it turns out, the Galilean transformations don’t play nice with this statement! Let’s see how this comes about.
Not always! You might have heard that “nothing can move faster than light.” As it turns out, the Galilean transformations don’t play nice with this statement! Let’s see how this comes about.
Consider an observer ![]() that is at rest. Object
that is at rest. Object ![]() is moving to the right with a velocity
is moving to the right with a velocity ![]() , where
, where ![]() is the speed of light, and observer
is the speed of light, and observer ![]() is moving left with velocity
is moving left with velocity ![]() . Plugging into the formula above, the velocity of
. Plugging into the formula above, the velocity of ![]() as measured by
as measured by ![]() is
is ![]() , a speed larger than the speed of light!
, a speed larger than the speed of light!
This seems very weird- our derivation seems airtight, yet clearly something went wrong. Let’s go through the derivation: first, we found how the various position vectors are related to each other. The drawing was simple and clear, so that part is clearly right. Then, we just “took the time derivative,” which also seems straightforward. So what is going on?
As it turns out, the fundamental problem is this: “take the time derivative” is not an unambiguous statement. In Einstein’s theory of relativity,
Time flows differently for different observers.
This phenomenom is often referred to as time dilation, and has been experimentally confirmed many times over. A particularly cool demonstration of this effect is the Hafele–Keating experiment, which you can learn about below if interested.
The bottom line is that the Galilean transformation we just derived is only approximately valid for objects that are moving slow to the speed of light. This is basically everything in our every day world. For instance, a rocket during launch achieves a speed of ![]() . That is enough to “climb Everest” in 1 second, but is still 200,000 times slower than the speed of light.
. That is enough to “climb Everest” in 1 second, but is still 200,000 times slower than the speed of light.
The Galilean transformations relate the velocities that different observers measure for the same object. For reasons I don’t really understand, physicists like to talk about reference frames, rather than “observers”, which seems much easier. As usual, since the vocabulary is standard, you should know that “reference frame” is just fancy speak for “observer.”
Let’s try two last exercises.
Exercise 14.3: Storm Chasing
You are on your car in a flat open field driving North at 30 mph. Using an instrument attached to your car, you determine that the tornado is moving in a North-Easterly direction, at a 45-degree angle to your right, at a speed of 10 mph. You need to determine the velocity of the tornado relative to the ground to determine whether it will hit a nearby town. What is the tornado’s velocity relative to the ground?
Exercise 14.4: Moving Cannons
A cannon shoots balls out at 60 mph. The cannon is mounted on a car, which drives right at 60 mph to the right The cannon points left, and is fired as the car is driving. How far from the location where it is fired will the cannon ball hit the floor? Explain your answer.
Turns out, the Myth Busters did this experiment.
To end, I will just like to point out one bit of miscellaneous information: if you are a road engineer, understanding relative velocities can be literally life saving. If that sounds surprising, check out the video below. I highly recommend Tom Scott’s channel, which is full of interesting videos about all sorts of random facts.
If you loved this material, and can’t wait to do more problems like these, I include below a challenge problem that is entirely optional.
Key Takeaways
You might expect the key takeaway here to be the Galilean transformation we derived
![]() .
.
However, it is much more important that you are comfortable with how we derived this relation.
One aspect of our derivation you really should remember: use different letters to signify quantities measured by different observers. This will be of tremendous help when solving problems.
Challenge Problem (Optional):
The problem below is challenging. If you feel like taking a challenge, try it out.
Andres is standing alongside a river whose water flows at 2 m/s. Ebony is standing 20 m upstream from Andres, on the other side of the river, which is 5 m wide. Ebony can swim at 1 m/s in still water. In which direction should Ebony try to swim so that she reaches the other side of the shore exactly at Andres’s position?
I think this is quite a difficult problem to think through, so if you want to try it by yourself, go for it. If you don’t get it (it is hard!), see if you can do it with my help.
Step 1: Draw a picture. Not a surprise, but drawing a good picture is probably the hardest part of this whole problem, for two reasons:
- We are told something about Ebony swimming in “still water”. That is, we know something about Ebony from the point of view of someone floating in the water. So, let’s imagine a leaf floating in the river. The leaf defines the water’s reference frame. Ebony’s speed in still water is simply Ebony’s speed as measured by that leaf.
- The second problem here is that, when I go to do the drawing, I instinctively want to place the origin at Ebony’s starting position. But that makes impossible to draw a position vector to Ebony at her starting place! Therefore, it is best to draw Ebony in the middle of her swim, so that we can see how everything is related throughout the problem (as opposed to just at the beginning!).
With these tips in mind, try making a complete drawing, including all relevant position vectors and labeling everything. Note you can arbitrarily set the direction of the river to the be x-axis, simplifying your picture. I got you started below. If you get stuck, you can reveal my answer by moving the slider.
Step 2: Find relations. Use your drawing to find relations. You should use all the information in the problem, so double check you have done so by going sentence by sentence through the problem (I find most people skip at least one vital piece of information when attempting this problem).
Step 3: Solve unknowns. This problem has a fair bit of algebra, and keeping everything straight can be hard. For that reason, I split the solution in two. Try figuring things out on your own first. If you can’t, open the first part of the solution. This will get you roughly halfway. Then try to finish the problem on your own.
If you’re still stuck at this point, you can find the second half of the solution below. When you reduce the problem to one equation with one unknown, it may not be obvious how to solve for the unknown (it isn’t!). Don’t worry about that. If you reduced the problem to one equation with one unknown, you solved the problem! You can plug the equation into Wolfram Alpha, and it will solve it for you immediately.
