44 Motion Subject to a Linear Force
In the last chapter, we solved some problems involving springs. However, in all the problems we considered, the spring length didn’t change. In this chapter, we set to study the dynamics of linear functions, i.e. problems for which the spring stretch is not constant.
Exercise 44.1: Motion Subject to a Linear Force
Consider the force 
with 
positive. Assume the particle starts at rest at position 
.
A. Assume 
. How will the object move when subject to the force 
?
B. Now let us assume we orient the x-axis such that 
. Assuming 
, how will the object start moving? Reason out how the object should move without doing any math.
C. Now consider the case 
. If the object starts at rest at , how will the object move in this case? If you get stuck, read through the first part of the solution, but then try finishing out the solution by yourself.
D. Given your answer to part C, can you guess the equation that describes the motion of this object?
In summary,
- An object at
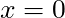stays there forever. We say 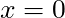is an equilibrium point. - If 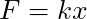, then nudging the object away from zero will cause it to shoot out to infinity. This makes 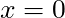an unstable equilibrium.
- Conversely, if
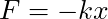, if we nudge the object away from 0, the force will push it back towards 0. We say 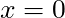is a stable equilibrium.
We also found that if a particle in a stable equilibrium is displaced from the equilibrium point, it oscillates around that equilibrium. Moreover, when , the resulting motion is precisely simply harmonic motion. This is a big deal: from Taylor series, any force 
that results in a stable equilibrium must look like if 
is small enough (i.e. we can neglect terms of order 
or higher). Consequently, oscillations around equilibrium points can be described using the equations from simple harmonic motion.
Key Takeaways
We considered the motion of an object subject to a force 
.