Springs

43 Springs

So far in this book we started by considering constant forces, or forces that were constant in magnitude, but not direction. We then discussed how, since forces are due to objects pushing on each other, solving the general case of non-constant forces can be quite difficult in general. We were, however, able to show that momentum is always conserved.

We now push bravely past the boundary of constant forces, and look at forces that change depending on the position of an object. We will, however, restrict ourselves to the simplest possible case: linear forces, i.e. forces of the form $F(x)=-kx$ . The simplest example of such a force is a spring, as shown below. We set $x=0$ at the equilibrium position of the spring.

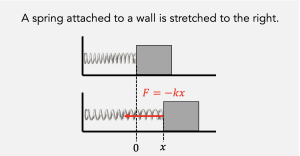
If the spring is stretched to the right a distance $x$ (so $x>0$ ), it pulls to the left, so $F<0$ . Conversely, if you compress the spring to the left ( $x<0$ ), the force will push to the right ( $F>0$ ). That is, the force always pushes in the opposite direction as the displacement. Experimentally, we also find that the strength of the push increases linearly with the displacement.

Putting it altogether one arrives at Hooke’s Law: $F_{\rm s}=-kx$ . The “s” subscript stands for “spring,” and the negative sign indicates the force is in the opposite direction of the displacement. From this point forth, we adopt Hooke’s law as our “theory of springs,” and so the equation goes in our tablets.

Just as with friction, our spring force law is only approximately correct. This is easy to see: if the length of the spring is $L$ at equilibrium, you certainly can’t compress the spring past a distance $L$ . Consequently, the theory can only be valid in the $x \ll L$ limit.

Important: In the equation $F_{\rm s}=-kx$ , the quantity $x$ has a very specific meaning, namely

$x$ is the distance the spring is stretched or compressed.

Consequently, if you wish to interpret the $x$ in Hooke’s law as a position, you must set the origin at the equilibrium position of the spring.

This is different from other situations, where you can set your origin wherever you please. If you’re dealing with springs, you set the origin at the equilibrium position of the spring. This is not really a law of physics, obviously, but if you fail to do so, you will generally make your life way harder.

Let us solve some problems involving springs.

Exercise 43.1: Hanging Out

A spring with spring constant $k$ and negligible mass is hung from the ceiling. You then hang a mass $m$ from the bottom end of the spring. The spring will stretch, bobbing up and down for a bit before settling down at an equilibrium point. Find the stretch $y$ of the spring at the equilibrium point. If you get stuck, you can use the slider to reveal my picture.

Exercise 43.2: Rotating Spring

A box of mass $m$ rests on a frictionless table. The mass is attached to one end of the spring of length $L$ when unstretched. The other end of the spring is nailed to the table. The spring is allowed to rotate freely about the nail.

You rotate the spring at an angular frequency $\omega$ , and measure that the spring stretches a distance $A$ . Find the spring constant of the spring. If you get stuck, use the slider to reveal my diagram.

Exercise 43.3: Weight on an Elevator.

Imagine a platform supported by two springs as shown. Assume the mass of the platform is negligible (i.e. you can set $m_{\rm platform}=0$ ), and that the two springs have identical spring constants $k$ where $k$ is known.

A. When you place an unknown mass $m$ on the platform, the springs are compressed by an amount $y$ that you can measure. Find the unknown mass $m$ in terms of $y$ . If you get stuck, check your drawing against mine by moving the slider below.

We have just invented a scale with which to measure weight!

B. Think carefully about the following question:

We can explicitly demonstrate that our balance measures the normal force on it by placing it in an elevator. Assume the elevator is in the first floor, and you press the button for the top floor. The elevator starts accelerating upwards with acceleration $a$ .

C. Will the balance read a mass $m'$ larger or smaller than the mass $m$ of the object? Explain.

D. Let $a$ be the acceleration of the elevator as it starts going up. Calculate the mass $m'$ that the balance will display as the elevator accelerates upwards.

Hint: since the mass of the platform is negligible, we can always set $m_{\rm platform}=0$ .

Optional: Robert Hooke. I’m always surprised at how much stuff Hooke accomplished during his life. In addition to physics, he contributed to geology, paleontology, horology, and biology. He used a new microscope (which he invented himself) to discover cells, and went on to make amazing drawings of insects that revolutionized British art. Just look at this drawing of a flea!

Key Takeaways

43 Springs

License

Share This Book