Displacement from Velocity

11 Displacement from Velocity

We have seen that velocity is the derivative of position: if we know $\vec r(t)$ , we can figure out $\vec v(t)$ . But can we go the other way around? The answer is yes, and the argument is actually pretty straightforward! Let’s go through it.

The bottom line from this discussion is that

Displacement is the integral of the velocity.

This is a very big deal! In particular, let’s write our final result, but explicitly setting $\vec v$ to $\vec d\vec r/dt$ inside the integral sign. We have

$\vec r(t_f) = \vec r(t_i) + \int_{t_i}^{t_f} \frac{ d\vec r}{dt} dt$ .

If we move $\vec r(t_i)$ to the left hand side of the equation, and define the change in position $\Delta \vec r \equiv \vec r(t_f) - \vec r(t_i)$ , we find

$\Delta \vec r = \int_{t_i}^{t_f} \frac{ d\vec r}{dt} dt.$

In other words, the change in position is the integral of the derivative. This is precisely the fundamental theorem of calculus! I discuss this connection in a bit more detail below.

The fundamental theorem of calculus

The fundamental theorem of calculus states that

$f(x_f) - f(x_i) = \int_{x_i}^{x_f} \frac{df}{dx} dx$ .

Notice how the left hand side of the equation is the change in $f$ , $\Delta f = f(x_f)-f(x_i)$ . On the right hand side, we are “summing up” the little tiny changes $df = (df/dx)dx$ of the particle as $x$ changes from $x_i$ to $x_f$ .

In other words, the total change in f is the sum of all the little tiny changes df as you move from $x_i$ to $x_f$ .

Hopefully you find this explanation of the fundamental theorem of calculus much easier to follow than what you saw in your calculus class: calculus “pops out” when thinking about how particles move. Indeed, both Newton and Leibniz were working on physics when they invented calculus!

The fundamental theorem of calculus is also important because it tells us that integrals are, in some sense, the inverse operation from a derivative, i.e. they “undo” a derivative. A derivative takes the function $f$ , and produces a new function $g$ . The integral takes the function $g$ , and returns the function $f$ . Note, however, that

we must always specify integration limits
the integral is the change in the function $f$ .

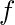Example: Compute the integral of $f(x)=x^2$ from $x_i=1$ to $x_f=2$ .

The integral is the function $F(x)$ such that, when I take its derivative, I get $x^2$ . But I know how derivatives of polynomials work! The derivative of $x^3$ is $3x^2$ , so I just need to multiply the whole thing by $1/3$ . Therefore,

$\int_1^2 x^2 dx = \tfrac{1}{3}x^3 \Big|_1^2 = \frac{7}{3}$ .

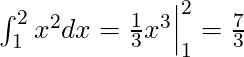Word of caution on notation: Consider the following integral appearing in the equation we just derived:

Integral = $\int_{t_i}^{t_f} \frac{ d\vec r}{dt} dt$ .

It is critically important that we fully appreciate this fact. The “integration variable” $t$ is just a dummy variable. I could just as easily have written

Integral = $\int_{t_i}^{t_f} \vec r'(x)dx$

where $\vec r'$ is the derivative of $\vec r$ . This is the exact same integral as what I wrote above. We can use anything as the integration variable.

In particular, suppose I wanted to find an expression for the position of a particle at time $t$ . Well, we already know the answer: if I simply set $t_f=t$ in our equation above, we’re done. Except for one little detail. Suppose we just set $t_f=t$ . Our equation reads:

$\vec r(t) = \vec r(t_i) + \int_{t_i}^{t} \frac{ d\vec r}{dt} dt$ .

This last equation, as written, doesn’t make sense. Notice that $t$ is both the integration variable, and the limit of the integral. Since we are interested in time $t$ , and the integration variable is a dummy variable, the correct way of writing this is:

$\vec r(t) = \vec r(t_i) + \int_{t_i}^{t} \frac{ d\vec r}{dt'} dt'$ .

This makes it clear that I’m interested in the position at time $t$ , and that the integral is over all times $t' \in [t_i,t]$ .

It is very easy to think “oh, I just integrate over time”, and then end up with equations that have $t$ both as a limit in the integral, and a dummy integration variable. And that inevitably leads to mistakes and confusion. It is critically important that you mind your notation when setting up integrals!

The trick is to remember that integration variables are dummy variables.

Exercise 11.1: Integrals Undo Derivatives

Use the fact that integrals “undo derivatives” to compute the function $F(t)$ .

$\bullet\ F(t) = \int_0^t (t')^n dt'$

$\bullet\ F(t) = \int_0^t \sin(\omega t')dt'$

$\bullet\ F(t) = \int_0^t \exp(t'/\tau) dt'$

$\bullet\ F(t) = \int_0^t \exp(-t'/\tau)dt'$

For the most part, I don’t really care if you do your integrals “by hand” or whether you use something like Mathematica or Wolfram Alpha to do your integrals. However, knowing some of these basic integrals (i.e. the ones above) by heart is very useful. Therefore, this problem is the exception to the rule: I want you to argue why you get the answer you get in English (see example in the green box above).

If you are feeling stuck, I include below the answer for the third bullet point. Try using the same type of reasoning to figure out the other three examples.

Rules of Integration- Linearity

One important bit that follows directly from the idea that integrals “undo” derivatives. Since multiplicative constants can slide past derivative signs, multiplicative constants can also slide past integral signs. That is,

$\int A f(t)dt = A \int f(t)dt$ .

This is something that you will use all the time.

Likewise, the fact that a derivative is linear (i.e. that it distributes past summation signs) also implies that integration is a linear operation. In other words, integrals also “slide past” addition (and subtraction) signs:

$\int [ f(t)+g(t)] dt = \int f(t)dt + \int g(t)dt$ .

Let’s use what we learned to derive some basic results.

Exercise 11.2: Calculating Position from Velocity

Consider a particle that moves with constant velocity $\vec v(t)=\vec v_0$ , and let $\vec r(t_i)$ be the initial position of the particle. Find the position of the particle at some arbitrary time $t$ later.

This is not exactly the most ground breaking result ever: note that $t-t_i$ is simply the total travel time $\Delta t$ . In other words, when moving at constant velocity, the total displacement is $\Delta \vec r = \vec v_0 \Delta t$ . This is exactly where we started! But- don’t be deceived. We have actually made a ton of progress, for we can now compute the displacement even when the velocity is not constant. Let’s look at the simplest such example:

Exercise 11.3: Motion With Constant Acceleration

A particle moves with a velocity that is constant in direction, but which increases linearly with time. Assuming that $\vec v = \vec v_0$ at time $t=0$ , and that we choose our coordinate system such that the $x$ -axis is in the direction in which the particle moves, we can write down the velocity of the particle as

$\vec v(t) = \left[ v_0 + at \right]\hat x$

where $a$ is a constant called the particle’s acceleration.

Letting $\vec r_0$ be the initial position of the particle, find the particle’s position at an arbitrary time $t$ later.

If the initial time is not $t=0$ , one can always set the initial time $t_i$ to zero by switching to a new time variable $\Delta t = t-t_i$ . In terms of $\Delta t$ , which now allows for an arbitrary initial time, we arrive at

$\vec r(t) = \vec r_i + (v_i \hat x) \Delta t + \frac{1}{2}(a \hat x) \Delta t^2$ .

I switched $\vec r_0$ to $\vec r_i$ since the initial time is no longer $t=0$ but rather $t_i$ . Note that $v_i\hat x$ is just the initial velocity $\vec v_i$ , while $a\hat x$ is the acceleration vector $\vec a$ , so that the above equation can be written as

$\vec r(t) = \vec r_i + \vec v_i \Delta t + \frac{1}{2}\vec a\Delta t^2$ .

It is not hard to convince yourself that this equation is also valid when $\vec v_i$ and $\vec a$ are arbitrary constant vectors by going over the above derivation one more time.

Word of caution: the result we derived above is often called the first kinematic equation. It is imperative to remember that the kinematic equation only applies for motion with constant acceleration. We will talk more about this later in the book.

Exercise 11.4: Calculating Position from Velocity

A particle starts at $x=x_0$ at $t=0$ . It’s velocity vector is given by $v(t)=v_0(t/\tau)^n$ , where $v_0$ , $\tau$ , and $n$ are all constants. Find $x(t)$ . I’ll walk you through the solution.

We start with the only thing we know: the relation between position and velocity, $dx=vdt$ .

Since we want $x$ , we integrate from the beginning of the story to the end of the story. To do this, you can think about the end of the story being some final time $t_{\rm f}$ (which you don’t know), and the particle ending at some position $x_{\rm f}$ (which you also don’t know). The point here is to give names to these quantities.

Note that on the left hand side of the integral, we have a “ $dx$ “. That means that the integration variable is $x$ . So: what is $x$ at the beginning of the story? What is $x$ at the end of the story? Use that to set the integration limits on the left hand side of the equation.

Conversely, on the right hand side of the equation we have a “ $dt$ “, which means that the integration variable is $t$ . What is $t$ at the beginning of the story? What is $t$ at the end of the story? Use this to set the integration limits on the right hand side of the equation.

Now that you have the integration limits, try doing the integral on the right hand side.

You can now bring it all together to find $x(t)$ . If you’re having trouble following my calculation, you can check out the video solution below.

Key Takeaways

The specific equation is: $\vec r(t) = \vec r_i + \int_{t_i}^{t_f} \vec v(t')dt'$

Practice Problems:

PP1: A particle starts at $x=x_0$ at $t=0$ . It’s velocity vector is given by $v(t)=v_0\exp(-t/\tau)$ , where $v_0$ and $\tau$ are constants. Find $x(t)$ .

PP2: A particle starts at $x=x_0$ at $t=0$ . It’s velocity vector is given by $v(t)=v_0\sin(\omega t)$ , where $v_0$ and $\omega$ are constants. Find $x(t)$ .

PP3: A particle starts at $x=x_0$ at $t=0$ .. It’s velocity vector is given by $v(t)=v_0/(1+t/\tau)$ where $v_0$ and $\tau$ are constants. Find $x(t)$ .

11 Displacement from Velocity

Practice Problems:

License

Share This Book