57 Energy is Not Conserved
So far we have looked at gravity and springs, and showed that in both cases we could define a potential energy such that the total energy was conserved. Let’s see if we can always do this. For simplicity, we will consider 1D only for now.
Exercise 57.1: Conservation of Energy
Consider an object that moves subject to a force ![]() that depends only on position. We saw that:
that depends only on position. We saw that:
- for a constant force
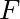 , the potential energy is
, the potential energy is 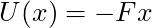 .
. - for a spring force
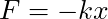 , the potential energy is
, the potential energy is 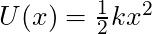 .
.
In each of these cases, ![]() . Let’s try to generalize this by defining
. Let’s try to generalize this by defining
![]()
where ![]() is some arbitrary reference point that we choose. For the constant force and spring forces in the last chapter we used the reference point
is some arbitrary reference point that we choose. For the constant force and spring forces in the last chapter we used the reference point ![]() .
.
A. Show that the work done by the function ![]() in taking a particle from
in taking a particle from ![]() to
to ![]() can be written as
can be written as ![]() .
.
This is a critical result, so I will state it again in bold: the work done by a force can be written as ![]() . We will use this result later in this book, so remember it.
. We will use this result later in this book, so remember it.
B. Plug the above expression into the work–energy theorem to prove that energy is conserved for objects subject to this force ![]() .
.
The above derivations shows that in 1D energy is conserved for any force that depends only on position. Interestingly, to define potential energy we had to select some reference point, but the reference point we choose doesn’t matter. This is why for gravity we can set ![]() wherever we want, and the conservation of energy equation will still hold.
wherever we want, and the conservation of energy equation will still hold.
At this point, it might look like we’re done. After all, we didn’t really make any assumptions about ![]() in the problem above: energy is always be conserved, right? Alas, there are more things in Heaven and Earth, Horatio, than are dreamt of in your philosophy. For example, wet toilet paper.
in the problem above: energy is always be conserved, right? Alas, there are more things in Heaven and Earth, Horatio, than are dreamt of in your philosophy. For example, wet toilet paper.
Exercise 57.2: Wet Toilet Paper
You get a wad of toilet paper all wet, and throw it at a wall. The toilet paper sticks to the wall.
Is energy conserved in this process? Explain your answer.
Because this collision did not conserve energy, we refer to it as an inellastic collision. Collisions that conserve energy (think a rubber ball hitting a wall instead!) are called elastic collisions. In practice, all real world collisions are inellastic, but some are approximately elastic, such as the example in the video below.
Bottom line: energy is not always conserved.
So what went wrong? As it turns out, not all forces have potential energies associated with them. Those that do are called conservative, and they satisfy conservation of energy. Those that do not are called non-conservative, and they do not conserve energy.
It may seem surprising that non-conservative forces can even exist. In the first problem in this chapter we found that any force ![]() that only depends on position conserves energy. Evidently, some forces depend on more than just position, and some of these do not conserve energy!
that only depends on position conserves energy. Evidently, some forces depend on more than just position, and some of these do not conserve energy!
Exercise 57.3: Non-Conservative Forces
Give an example of a force ![]() that depends on more than just the position of an object. Justify your answer.
that depends on more than just the position of an object. Justify your answer.
Now that we know that non-conservative forces exist, let’s look at what these forces do to the conservation of energy equation.
Exercise 57.4: Energy is Not Conserved
An object is subject to two forces, a conservative force ![]() with potential energy
with potential energy ![]() , and a non-conservative force
, and a non-conservative force ![]() . Starting from the work–energy theorem, derive the conservation of energy equation in the presence of non-conservative forces.
. Starting from the work–energy theorem, derive the conservation of energy equation in the presence of non-conservative forces.
We have finally arrived at our full conservation of energy equation! Energy is conserved, unless there are non-conservative forces that do work. However, “non-conservative” is too cumbersome to use as a subscript, so I will use “noncon” instead.
![]()
You can see that this looks an awful lot like the conservation of momentum equation, ![]() . In both cases, we have a quantity that is conserved unless some other force comes in and messes things up.
. In both cases, we have a quantity that is conserved unless some other force comes in and messes things up.
Warning: In the momentum equation, momentum is conserved unless there are external forces. I have found students often latch onto this, and then want to make statements like “Energy is conserved unless there is external work.” This is incorrect. Conservation of energy has nothing to do with whether the work done is external or not. What the energy equation cares about is work done by forces with no potential energy (non-conservative forces).
Make sure you keep which is which when solving problem. If you remember the equations with subscripts — ![]() for momentum,
for momentum, ![]() for work — that will help.
for work — that will help.
Our final equation for conservation of energy is a big result and a law of physics, so we add it to our tablets.

Let’s make sure we can use this form of the conservation of energy equation to solve a problem.
Exercise 57.5: Sliding Down a Ramp
A ramp makes an angle ![]() with the horizontal. A block of mass
with the horizontal. A block of mass ![]() starts a distance
starts a distance ![]() from the bottom of the ramp (the distance
from the bottom of the ramp (the distance ![]() is measured along the ramp). The kinetic frictional coefficient between the block and the ramp is
is measured along the ramp). The kinetic frictional coefficient between the block and the ramp is ![]() . Assuming the block starts sliding down the ramp, how fast will it be moving when it reaches the bottom of the ramp?
. Assuming the block starts sliding down the ramp, how fast will it be moving when it reaches the bottom of the ramp?
We’ll walk through this together.
Step 0: What’s the story? Does the story have a beginning and end? Is this a before and after problem?
Step 1: Draw a picture. Draw both a “before” and an “after” picture, and label everything. Your drawing should include a force diagram of the forces that are acting during the story.
Steps 2 and 3: Find relations and solve. From step 1, we already know that this is a conservation of energy problem, so start there. Notice, however, that your force diagram contains two forces that don’t have a potential energy associated with them. These forces are non-conservative. Make sure you compute the work done by each of the two forces.
At this point you might not be too impressed: after all, you could have solved the previous problem using the kinematic equations and Newton’s law. However, it’s way easier to solve this problem using conservation of energy. What’s more, you can also solve new problems that you couldn’t have solved before! Let’s take a look.
Exercise 57.6: Sledding Downhill.
A skier is at the top of a hill of height ![]() as shown below. We will assume that the friction between the skis and the snow is negligible. Assuming the skier just lets himself slide down by gravity, how fast will he be moving by the time he reaches the bottom of the slope?
as shown below. We will assume that the friction between the skis and the snow is negligible. Assuming the skier just lets himself slide down by gravity, how fast will he be moving by the time he reaches the bottom of the slope?
We’ll go through this slowly.
Step 0: What’s the story? Is this a before and after problem? What’s the beginning, and what’s the end? What do we need to do solve the problem?
Step 1: Draw a picture. Make sure you clearly have a before and after labelled, and that your picture includes a force diagram.
Steps 2 and 3: Find relations and solve. Set up the conservation of energy equation, and make sure you account for the work done by any non-conservative forces in your diagram.
We can see that our final answer for problem 57.6 is the same as for problem 57.5, which is remarkable! In 57.5 we had an object moving down a ramp: nice and simple. This time around, however, the shape of the slope is complicated, so the acceleration is always changing; unlike problem 57.5, we can’t use the kinematic equations to solve this problem. By contrast, conservation of energy still applies, and the fact that the motion during the story is complicated is completely irrelevant. Behold the power conservation laws!
Key Takeaways
