46 Linear Forces and Simple Harmonic Motion
We argued in chapter 44 that an object subject to the force ![]() can be described as simple harmonic motion. Let’s now show that this is indeed the case. Before we do so, we’ll need to become familiar with some standard physics notation when it comes to derivatives.
can be described as simple harmonic motion. Let’s now show that this is indeed the case. Before we do so, we’ll need to become familiar with some standard physics notation when it comes to derivatives.
Notation: Spatial and Time Derivatives
Consider a function ![]() that depends on a spatial coordinate
that depends on a spatial coordinate ![]() . The derivative of
. The derivative of ![]() is written as
is written as ![]() . However, we often use the shorthand notation
. However, we often use the shorthand notation ![]() . This “prime” notation is standard, and you probably saw it in your math class.
. This “prime” notation is standard, and you probably saw it in your math class.
In physics, however, we distinguish between derivatives with respect to space, and derivatives with respect to time. For derivatives with respect to time, we don’t use a prime, but rather a “dot” over the function. So, if ![]() is a function of time, then we write
is a function of time, then we write ![]() and
and ![]() .
.
This “dot” notation is standard, and needs to become part of your math vocabulary.
Exercise 46.1: Mass on a Spring
One end of a spring of constant ![]() is attached to a wall. The other end is attached to a block resting on a frictionless table. You grab the block, pull it a distance
is attached to a wall. The other end is attached to a block resting on a frictionless table. You grab the block, pull it a distance ![]() to the side, and then let it go. Determine its position as a function of time.
to the side, and then let it go. Determine its position as a function of time.
We will walk through this solution slowly. Before we get going with math, we should figure out what’s going on. Start by describing how the object will move in English.
Now make a drawing of the block at some distance ![]() . If you get stuck, you can take a look at my picture. As usual, include all forces acting on the object in your drawing.
. If you get stuck, you can take a look at my picture. As usual, include all forces acting on the object in your drawing.
Now find relations and solve. Here is a useful rule for this class:
Whenever we are trying to determine how an object moves, the starting place is always Newton’s law.
Use your picture to setup Newton’s laws for each axis. When doing so, you will run into one subtle point: in our picture, the acceleration points left, so you may be tempted to write ![]() , and then solve for the magnitude of the acceleration
, and then solve for the magnitude of the acceleration ![]() . This works when the acceleration of an object is constant. However, in this problem the acceleration is not always left, so we need to write
. This works when the acceleration of an object is constant. However, in this problem the acceleration is not always left, so we need to write ![]() (with no minus sign). As we will see, Newton’s equations will take care of the sign for us.
(with no minus sign). As we will see, Newton’s equations will take care of the sign for us.
Setup Newton’s equation along the ![]() -axis, and use the fact that acceleration is the second derivative of the position to get an equation that looks like
-axis, and use the fact that acceleration is the second derivative of the position to get an equation that looks like ![]() .
.
Because the equation we ended up with involves the derivatives of a variable, it is referred to as a differential equation. Our goal is to find the solution ![]() that satisfies this equation. Use your understanding of how the block will move to guess the solution of this equation.
that satisfies this equation. Use your understanding of how the block will move to guess the solution of this equation.
Try plugging in your guess into the differential equation. Can you pick the value of ![]() to make sure your guess is a solution?
to make sure your guess is a solution?
Find the period of the oscillation. How does this period depend on the initial displacement ![]() of the block?
of the block?
This is surprising! If an objects starts further out, it must travel a larger distance, so one might expect the period to go up. However, the larger displacement results in a stronger push, which makes the object move faster. Evidently, the two effects exactly cancel each other out. As it turns out,
The fact that the period of oscillations is independent of the amplitude is a unique feature of simple harmonic motion.
There are three key lessons that I want you to take away from the previous problem.
- Whenever you have a differential equation of the form
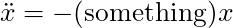 , the solution is simple harmonic motion.
, the solution is simple harmonic motion. - Whatever the “something” is that appears in front of
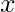 , that “something” is the square of the angular frequency. For springs, this means
, that “something” is the square of the angular frequency. For springs, this means 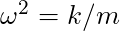 .
. - The period of a simple harmonic oscillator is independent of its amplitude.
The fact that the angular frequency for a mass on a spring is given by ![]() is a useful result that we need to know, and so it goes in our tablets.
is a useful result that we need to know, and so it goes in our tablets.
 Let’s try a problem to test whether we really learned the lessons above.
Let’s try a problem to test whether we really learned the lessons above.
Exercise 46.2: Finding the Frequency
You poke a hole through a board, stick a string through it, and then use it to hang a boot from a table. The boot has a mass ![]() and a moment of inertia
and a moment of inertia ![]() . The distance from the point from which the boot is hung to the center of mass of the boot is
. The distance from the point from which the boot is hung to the center of mass of the boot is ![]() . The oscillations of the boot are described by the following differential equation:
. The oscillations of the boot are described by the following differential equation: ![]() .
.
Find the period of the boot’s oscillations.
Key Takeaways
