Describing Circular Motion

35 Describing Circular Motion

When a particle moves in a circle it is useful to describe the position of the particle in term of an angle, e.g. the angle the particle makes with the x-axis. As the particle moves, the angle changes, which results in angular motion. Our goal in this chapter is to connect the angular motion of an object with its linear motion.

Exercise 35.1: Angular Velocity

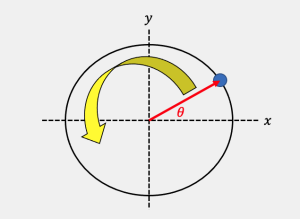Consider now an object moving in a circle of radius $r$ with constant speed $v$ as depicted in the picture at right. We define $\theta$ as the angle that the radial vector pointing to object makes with the x-axis, as shown. We further assume the object starts at $\theta=0$ at $t=0$ .

A. Find an expression for $\theta(t)$ .

B. Just as (velocity) $\times$ (time) = distance, we can define the angular velocity (usually denoted by the letter $\omega$ ) at which the particle is moving around in a circle such that

(angular velocity) $\times$ (time) = angle swept.

Use your expression for $\theta(t)$ to determine the object’s angular velocity $\omega$ .

C. Let us take another look at angular velocity. Image we define $l$ as the linear distance travelled by the particle. Then, we know $l=r\theta$ , as long as $\theta$ is measured in radians. Clearly, the object’s speed at any time is $v=dl/dt$ . By the same token, the angular velocity can be defined as $\omega \equiv d\theta/dt$ .

Use the fact that $l=r\theta$ to find the relation between linear and angular velocity for an object in circular motion.

D. Consider the linear velocity of the object at the top of the circle.

For this reason, rather than writing $v=r\omega$ , I will write $v_{\rm tan}=r\omega.$ This can help us remember that we’re talking about a tangential velocity.

E. The angular acceleration $\alpha$ is the rate of the angular velocity with respect to time, $\apha \equiv d\omega/dt.$ . How will the tangential acceleration be related to the angular acceleration?

The relation $v_{\rm tan}=r\omega$ is one that you absolutely must know. However, as you saw above, this relation is nothing else than the derivative of $l=r\theta$ , which I expect you are already very familiar with. That is, the equation $v=r\omega$ is not really a new equation, and for that reason I’m not adding to our tablets: if you remember $l=r\theta$ , you’re already good to go!

Exercise 35.2: A Surprising Relation

Consider again a ball moving in a circle, same as last problem. We now wish to focus on how the $x$ and $y$ coordinates of the ball are changing with time.

A. Using plain English, describe the motion of the ball along the x-axis ( ignore the y-axis entirely).

B. Let $r$ be the radius of the circle. Find $x(t)$ and $y(t)$ for a particle moving in a circle at constant speed. Do you recognize those equations? Does this make sense given your description of the motion in part A of this question?

C. Summarize your results as a single sentence relating circular motion to simple harmonic motion.

This is really cool to watch!

Bottom line: uniform circular motion can be thought of as simple harmonic motion along the x and y axis simultaneously.

D. How does the angular velocity of the circular motion compare to the angular frequency of the oscillators along the x and y axis?

E. Complete the following sentence:

Let’s try one last question.

Exercise 35.3: Which Way?

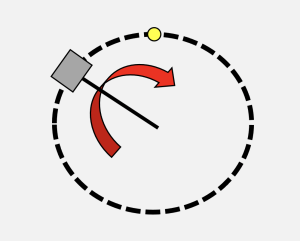Imagine a box on a frictionless table. The box is tied to a rope, and is spun around so that it is going around clockwise in a circle as viewed from above (see figure at right). The centripetal force for the circular motion is provided by the tension of the string.

This can be beautifully demonstrated by putting a sparkler on a drill!

Original video here.

The main thing to take away from this discussion is this: left alone, objects move in a straight line. An object in uniform circular motion is obviously not moving in a straight line, and so there must be a force keeping it in that circular motion: remove the force, and the object will go back to moving in a straight line.

Optional- the bit in this box is most definitely not required, so you can skip it if you want. It’s pretty fun though!

We have argued that if an object is moving in circular motion and you remove the centripetal force acting on the object, the object will “fly off” in the tangent direction. This is true, but that fact that information travels at a finite speed can lead to some surprising conclusions!

Suppose you have a ball on a string, and you spin it around in a circle. If you let go of the string, it takes a tiny amount (milliseconds!) of information to reach the object. That means that there is a time delay between you letting go off the string, and the tension on the ball disappearing. After you let go of the string, but before the tension disappears, the tension force will continues to keep the ball in circular motion. It’s a small effect, but can be made larger by slowing down how fast information can travel, e.g. by using a slinky. Check it out! Original video can be found here.

I think that’s amazing!

As it turns out, the idea that information travels at a finite speed is central to Einstein’s theory of relativity. Weirdly, however, quantum mechanics seems to allow for information to travel at infinite speeds. So something somewhere is wrong, but we haven’t figured it out yet.

Key Takeaways

35 Describing Circular Motion

License

Share This Book