The Relation Between Energy and Force

60 The Relation Between Energy and Force

I want to revisit some of the mathematical formalism having to do with potential energy. You will recall that if a force $F$ depends only on position then we could define a potential energy function

$U(x;x_0) = - \int_{x_0}^x F(x')dx'.$

This potential energy function explicitly depends on the reference point $x_0$ , which is why I am writing $U(x;x_0)$ in the equation above. Now, suppose that we changed the reference point from $x_0$ to some other point $x_0'$ . The new potential energy would be

$U(x;x_0') = - \int_{x_0'}^x F(x')dx'.$

But- to go from $x_0'$ to $x$ , we could imagine stopping at $x_0$ in the middle. This allows us to split this integral in two

$U(x;x_0') = - \int_{x_0'}^{x_0} F(x')dx' - \int_{x_0}^{x} F(x')dx'$ .

The first integral is just some constant number, let’s call it $U_{\rm offset}$ . The second integral above is just the potential energy $U(x;x_0)$ . In other words, the relation between the new and old potential energies is

$U(x;x_0') = U_{\rm offset} + U(x;x_0)$ .

So which is correct? The answer is both! Changing the reference point changed the potential energy by a constant value $U_{\rm offset}$ . Since this constant is added to both the initial and final potential energies in the conservation of energy equation

$E_{\rm f} = E_{\rm i} + W_{\rm noncon},$

we can see that the conservation of energy equation still works! This means that: 1) you can choose any old reference point you want when defining potential energy; and 2) you are always free to add any arbitrary constant to your potential energy definition, and everything still works out. Put another way, if you want to say that you have a potential energy of 1-bijillion Joules, you can do so, and no one can tell you otherwise.

Let’s try a problem illustrating these results.

Exercise 55.1: Zero points

A. As a good physicist studying gravity, you have set $y=0$ to the floor of the room, and you have defined your gravitational potential energy $U(y)=mgy$ . Your friend is interested in doing some experiments on a table of height $h$ . Consequently, she sets a new coordinate system with $y'=0$ at the height of the table. Evidently, $y'=y-h$ .

Determine how the gravitational potential energies $U(y)$ and $U(y')$ are related to each other. Which of the two energy functions is correct? Explain your answer.

B. Now suppose you have a spring. You set up your coordinate system such that $x=0$ when the spring is neither stretched nor compressed. The potential energy in the spring when it is stretched to a new $x$ is $U(x)=\frac{1}{2}kx^2$ . A second friend comes along, and they decide they want to set the origin of their coordinate system ( $x'$ ) some distance $a$ to the right of the equilibrium point, so that $x'=x-a$ . They then set the potential energy of the spring to $U(x')=\frac{1}{2}k(x')^2$ . Is your friend allowed to do that? Explain your answer.

An interesting by product of these observations is that the value of the potential energy does not have a physical meaning. However, changes in the potential energy do have physical significance. Thus, while you may well say that an apple on the table has either zero energy or maybe 1-bijillion joules of energy, if you raise that apple by 1 m, then the change in the apple’s energy is $\approx 1\ {\rm J}$ regardless.

The fact that only changes in potential energy have a physical significance can be made even more explicity by going back to the definition of potential energy,

$U(x;x_0) = - \int_{x_0}^x F(x')dx'.$

If we take the differential on both sides of this equation, we arrive at

$dU=-dW$ ,

where $dW$ is the work done by the force with potential energy $U$ . This is simply another way of saying what we found before: work is minus the change in potential energy. This brings us finally to the big point of this chapter: what is the relation between energy and force?

Exercise 55.2: The Relation Between Force and Potential Energy

Consider the relation $dU=-dW$ . Suppose you have a force $F$ with potential energy $U$ . Use the fact that you know the relation between potential energy and work to find an expression for the force $F$ in terms of the potential energy function $U$ .

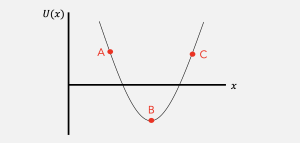
Let’s make sure the lesson here was learned. Consider an arbitrary force $F(x)$ , whose potential energy function is given by the diagram below.

When working in multiple dimensions, the “force is the derivative of the potential” gets generalized in a very natural way. For instance, in two dimensions you end up with

$\vec F = - \nabla U = -\left[ \frac{\partial U}{\partial x} \hat x + \frac{\partial U}{\partial y}\hat y \right].$

We won’t really be doing anything with this in this textbook, but hopefully you can see this is pretty much the simplest way to generalize things: the force along the x-axis is the x-derivative of the potential, while the force along the y-axis is the y-derivative.

Let’s do a sample problem where we use what we just learned about forces and potential energy.

Exercise 55.3: Force and Potential Energy

The potential energy of a force $F(x)$ is given by $U(x) = \U_0 a^{-3}x(x-a)(x+a)$ where $U_0$ and $a$ are both constant.

A. Find the units of $U_0$ and $a$ . Justify your answer.

B. Sketch U(x), and clearly mark the regions of space in which the force points left, and the regions of space in which the force points right.

C. Calculate the force $F(x)$ . Does your expression agree with what you found in part A of the problem?

D. Recall that an equilibrium point is a point where the force $F=0$ . Explain why these points are called equilibrium points, and find the equilibrium points for this force.

E. Imagine placing a particle the equilibrium point to the left of $x=0$ . If you take the particle, and displace it slightly to the right, will the particle experience a force towards or away from the equilibrium point? What about if you displace the particle slightly to the left instead? What does this tell you about how the particle moves if you slightly nudge it away from the equilibrium point?

F. Now imagine placing a particle the equilibrium point to the right of $x=0$ . If you take the particle, and displace it slightly to the right, will the particle experience a force towards or away from the equilibrium point? What about if you displace the particle slightly to the left instead? What does this tell you about how the particle moves if you slightly nudge it away from the equilibrium point?

G. Equilibrium points can be classified into stable and unstable equilibrium. Based on your answer in parts D and E, which equilibrium points in the curve are stable, and which are unstable? Explain your answer.

The idea of equilibrium points is a pretty important one. As you found in the problem above, stable equilibria look like bowls in the potential energy function, whereas unstable equilibria look like hills. This makes sense: displace a ball from the bottom of the bowl, and it’ll roll back to the bottom; displace the ball from the top of a hill, and it rolls away.

Interestingly, 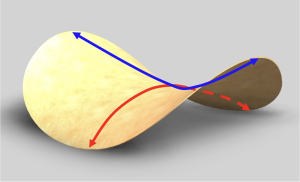in 3-dimensions it’s possible to have mixtures of these two, called saddle points. These occur when the potential energy $U(x,y)$ has a minimum along one axis, but a maximum along the other axis (e.g. a pringle!). Mathematically, this means that the equilibrium point of a saddle point is stable in one axis, and unstable along the other axis. In practice, however, you can never nudge a particle perfectly along one axis. That is, you can’t really balance a marble on a pringle.

In summary, the value of the potential energy has no physical significance: only changes in potential energy have a physical meaning. This is reflected in the definition of energy, $dU=-dW=-Fdx$ . Dividing by $dx$ , we find $F=-dU/dx.$ That is, force is minus the derivative of the potential. This means forces push things towards places with lower potential energy. This basic idea that things want to “move to lower energy” is an important concept, one that is central to pretty much all of chemistry, as well as quite a bit of physics.

Key Takeaways

60 The Relation Between Energy and Force

License

Share This Book