Simple Harmonic Motion

10 Simple Harmonic Motion

Let’s practice translating English into math while working on velocities by looking at the most important problem in physics: simple harmonic motion.

Imagine hanging a mass on a spring. If you pull on the mass and let go, the mass bobs up and down under the combined action of gravity and the spring. This “bobbing up and down” is called simple harmonic motion. We’d like to find a function that can describe the bobbing up and down mathematically.

What is a function that goes up and down over and over again?

We can reveal this functional form by replacing the mass on the spring by a can of spray paint, and dragging a piece of paper behind the can, as shown below (demo by the MID Dept. of Physics, original video can be found here).

An object whose position can be described using a sine or a cosine function is said to be undergoing simple harmonic motion.

But what exactly does this look like in terms of an equation? We can’t write something like $y(t)=\sin(t)$ : the sine function takes as inputs angles, and angles are not measured in seconds! What we need is to multiply the $t$ inside the sine function by a number that gets rid of the units of second, and turns the whole thing in an angle. The equation to describe simple harmonic motion is therefore

$y(t)=A\cos(\omega t)$

where $y$ is the height of the mass bobbing up and down, and $\omega$ is a quantity that has units of (radians/time). The quantity $\omega$ is called the angular frequency, and makes it so that $\omega t$ has units of radians. The angle that goes in the sine/cosine functions is called the phase angle. In the next exercise, we examine this expression in detail to make sure we fully understand it.

Exercise 10.1: Describing Simple Harmonic Motion

Consider a mass bobbing up and down in simple harmonic motion. The height of the mass relative to the “middle” is given by $y(t)=A\cos(\omega t)$ , where $A>0$ .

Since the mass is bobbing up and down, the motion of the mass is periodic. That is, it repeats itself after some time $T$ , which we call the period of the oscillation. What angle corresponds to “one full oscillation” ? (Hint: think about what the cosine function looks like!)? Use your answer to find how $\omega$ is related to the period $T$ of the oscillation.

If you struggled, you can see the solution below.

In summary: in simple harmonic motion, objects oscillate back and forth in a sinusoidal fashion, e.g. $y(t)=A\cos(\omega t)$ . The meaning of each of the key parameters are:

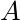$A$ is the amplitude, the maximum displacement from the middle point of the oscillation.
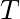$T$ is the period, the time it takes for the motion to repeat itself.
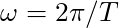$\omega = 2\pi/T$ is the angular frequency.

The equation for $\omega$ comes up in many different contexts, so you have two options: 1) memorize it; or 2) understand why this equation is true, so you don’t have to memorize it! As long as you remember that $\omega T$ is the angle required to “restart” the oscillation, you can quickly figure out that $\omega T=2\pi$ , no memorization required.

Let’s turn now to the velocity of an object in simple harmonic motion. As an object bobs up and down its velocity is fluctuating: half the time the particle is moving up, and the other half it is moving down. Thus, we might expect the velocity to look something like a sine or a cosine function. To calculate this velocity, we will need two more rules for derivatives (you can skip the green boxes if you’re comfortable with calculus):

The Derivative of an exponential, and the sine and cosine functions

The derivative of the functions $\exp(x)$ , $\sin(x)$ , and $\cos(x)$ are as follows:

• $\frac{d}{dx}\exp(x)=\exp(x)$ .

• $\frac{d}{dx}\sin(x) = \cos(x)$ .

• $\frac{d}{dx}\cos(x) = -\sin(x)$ .

The justification for these statements is “that’s what we get when we apply the definition of a derivative.” As before, for the purposes of this class, you just need to remember these rules.

Rules of Derivatives: the chain rule

The chain rule allows us to compute the derivative of a “nested” function. It goes as follows:

Given $g(t) = f( {\rm Function}(t))$ , to evaluate the derivative of $g$ you need to:

Evaluate the derivative of $f$
Multiply the derivative of $f$ by the derivative of the thing inside the parenthesis.

Example: Let’s compute the derivative of $g(t)=\exp(-(t/\tau)^2)$ with respect to $t$ .

$\circ$ The derivative of $\exp(x)$ is just $\exp(x)$ .

$\circ$ The thing inside the parenthesis is $F(t)=-(t/\tau)^2$ , which has a derivative $F'(t)=-2t/\tau^2$ .

$\circ$ Putting it all together, we get

$\frac{d}{dt}\left[ \exp(-(t/\tau)^2 )\right] = \exp( -(t/\tau)^2 )\times (-2t/\tau^2)$

The chain rule is an absolutely essential piece of calculus that you must master in order to be able to do physics.

Exercise 10.2: The Velocity of an Object in Simple Harmonic Motion

A mass bobs up and down in simple harmonic motion, with $y(t)=A\cos(\omega t)$ . Calculate the function $v(t)$ that describes the velocity of the mass.

Use you answer to find an expression for the maximum velocity $v_{\rm max}$ of the mass as it bobs up and down. As a specific example, let’s assume that the amplitude of the oscillation is $A=5\ {\rm cm}$ , and that the period of the oscillation is $2\ {\rm s}$ .

Exercise 10.3: Practice with Simple Harmonic Motion

In all of the examples above, we have assumed $y(t)=A\cos(\omega t)$ , which has the mass starting at its maximum displacement at $t=0$ .

A. What equation describes the position as a function of time of the mass if we assume that the mass is crossing the middle line moving downwards at $t=0$ instead?

B. Find the corresponding expression for the velocity.

Key Takeaways

10 Simple Harmonic Motion

License

Share This Book