Solving a System of Equations

Solving a System of Equations

To read this book you will need to be comfortable with solving systems of equations. We’ll go through how to do this within the context of a specific problem first.

Example: Solving Systems of Equations

For example, consider two equations with two unknowns $x$ and $y$ given by

$2x+3y = 5$

$4x-2y = 1$

Find $x$ .

Solution: The first thing we notice is that if we want to solve $x$ , we don’t care about $y$ . Therefore, we have to get rid of $y$ .

Here is the key insight: if the coefficient of $y$ is the same in both equations, we can add/subtract the two equations to get rid of $y$ .

To make the coefficient of $y$ of the two equations the same, we can just multiply each equation by the appropriate coefficient.

Let’s see this in action. In this case, we see the coefficient of $y$ in the first equation is 3. So- let’s multiply the second equation by 3. Likewise, the coefficient of the second equation is 2 (before we mess with it), so we multiply the first equation by 2. This makes the coefficient of both equations “6”.

$4x+6y=10$

$12x-6y=3$

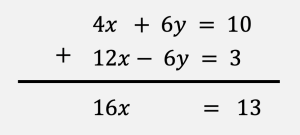Since the coefficients of $y$ match with opposite signs, we add the two equations. I like to “line up” the equations so that each “column” has only one kind of variable as shown in the picture below.

At this point, we have one equation with one unknown, which can easily solve. In this case, $x=13/16$ .

If we need to find both $x$ and $y$ , now that we know what $x$ is, we can substitute $x$ in either of our original two equations, and solve for $y$ .

In the example above, I use numerical coefficients in front of $x$ and $y$ to make the algebra look less intimidating, but please notice that the pattern we followed doesn’t care at all about what the coefficient in front of $y$ is.

In other words, the method for solving these equations is:

Identify the variable you do NOT care about.
Multiply equation 1 by the coefficient of “variable you don’t care about” in equation 2, and multiply equation 2 by the coefficient of “variable you don’t care about” in equation 1.
Add/Subtract the two equations to get rid of the variable you don’t care about.

To help you remember this, you can summarize this whole thing simply as the “add equations to get rid of variables you don’t care about” method.

Exercise: Solving Systems of Equations

To make sure we get it, let’s solve the most general form of two linear equations with two unknowns. That is, we will solve for both $x$ and $y$ in the following set of equations.

$ax+by=e$

$cx+dy=f$

What if we had three equations with three unknowns? The method is exactly the same. Say the unknowns are $x$ , $y$ , and $z$ . You want to solve for $x$ . Here’s how we do it.

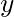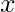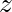Choose two of the original equations. Use these two equations to get rid of one of the variables you don’t care about (e.g. $y$ ). This gives you one new new equation with only $x$ and $z$ in it.
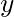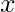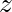Now choose another set of two of the original equations. Once again, get rid of $y$ . This gives a second new equation with only $x$ and $z$ in it.
The two new equations from step 1 and 2 are a system of two equations with two unknowns, which you already know how to solve!

Ta-daa! Using the “add equations to get rid of variables you don’t care about” method we’ve solved a system of three equations with three unknowns.

Note too that if in the original set of 3 equations there is one equations that only has two unknown variables, then you just saved yourself a step. Choose the other two equations, and get rid of the “third” variables. Let’s do an example.

Exercise: Three Equations with Three Unknowns.

Solve for $x$ in the following set of equations.

$a_1 x + b_1 y = d_1$

$b_2y + c_2z = d_2$

$a_3 x + c_3 z = d_3$

Solving a System of Equations

License

Share This Book