Acceleration

16 Acceleration

Newton’s laws tell us that when you push or pull an object, its velocity will change. Therefore, we must learn how to describe changes in velocity. Fortunately, this is a simple generalization of work that we have already done!

Exercise 16.1: The Definition of Acceleration.

Recall that velocity tells us how position changes over time, i.e. $d\vec r = \vec v dt$ . Here, $d\vec r$ is the change in position in time $dt$ . This was our definition of velocity. We define acceleration in a completely analogous way, only now we are interested in characterizing the change in velocity $d\vec v$ in some amount of time $dt$ . Use this discussion to define acceleration. What are the units of acceleration?

Notice that our definition of “acceleration” does not quite match the colloquial use of the word, which usually signifies that the speed of an object is increasing. By contrast, in physics the word “acceleration” is not limited to “going faster.” Any change of the velocity vector is referred to as acceleration.

Exercise 16.2: What is Acceleration?

Let’s try our hand at answering some quick yes/no questions.

Exercise 16.3: Relating Velocity and Acceleration

Now let’s do some math. We have defined acceleration such that $d\vec v = \vec a dt$ .

Use this equation to find:

An equation relating acceleration to the derivative of velocity.
An equation relating changes in velocity to the integral of acceleration.

I have found the above bit can be difficult for students at first, so let’s make sure we’re comfortable with getting velocity from acceleration by doing a problem.

Exercise 16.4: Calculating Velocity from Acceleration

Suppose a particle starts at $x=x_0$ with velocity $v=v_0$ at time $t=0$ . It’s acceleration is given by $a(t)=a_0 (t/\tau)^n$ where $a_0$ , $\tau$ , and $n$ are all positive constants. Find $v(t)$ and $x(t)$ .

Try doing this problem on your own first. The hint I can give you is that the procedure here is identical to what we did to find position from velocity.

If you find yourself struggling, here’s a walk through. If you need the walkthrough, make sure you try the practice problems at the end of this chapter as well.

Walkthrough part I: We start from the relation between acceleration and velocity, $dv=adt$ . Set up the integrals making sure you go from the beginning of the story to the end of the story.

Walkthrough part II: Now do the integral on the right hand side to find the final expression.

Putting it all together, we arrive at

$v(t) = v_0 + \large\frac{a_0\tau}{n+1}\left( \frac{t}{\tau}\normalsize \right)^{n+1}.$

To find $x(t)$ , you now need to start from the relation between position and velocity. This is exactly what you did in problem 11.4. Try it on your own.

Exercise 16.5: Reading Acceleration from Velocity vs Time Graphs

In the previous exercise, you found that acceleration is the derivative of velocity, i.e. $\vec a = d\vec v/dt$ . If an object is moving in one direction (so that we can omit the vector sign), we have simply $a=dv/dt$ .

Imagine you made a plot of $v$ on the y-axis, and $t$ on the x-axis. How is the acceleration related to this graph?

Let’s try a couple of questions to make sure we’re all in the same page. These questions are all based on the four graphs below.

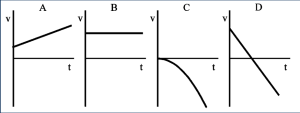
Key Takeaways

Starting from the base equation $d\vec v = \vec a dt$ , we can:

$\bullet$ Divide by $dt$ to arrive at $\vec a = \frac{d\vec v}{dt}$ .

$\bullet$ Integrate to arrive at $\vec v(t) = \vec v_i + \int_{t_i}^{t_f} \vec a(t')dt'$ .

Practice Problems:

PP1: A particle starts at $x=x_0$ with velocity $v=v_0$ at time $t=0$ . It’s acceleration is given by $a(t)=-a_0\exp(-t/\tau)$ where $a_0$ and $\tau$ are positive constants. Find $v(t)$ and $x(t)$ .

PP2: A particle starts at $x=x_0$ with velocity $v=v_0$ at time $t=0$ . It’s acceleration is given by $a(t)=a_0\cos(\omega t)$ where $a_0$ and $\omega$ are positive constants. Find $v(t)$ and $x(t)$ .

PP3: A particle starts at $x=x_0$ with velocity $v=v_0$ at time $t=0$ . It’s acceleration is given by $a(t)=a_0/(1+t/\tau)$ where $a_0$ and $\tau$ are positive constants. Find $v(t)$ and $x(t)$ .

16 Acceleration

Practice Problems:

License

Share This Book