Acceleration Practice

17 Acceleration Practice

Let’s do multiple practice problems to get more comfortable with the concept of acceleration.

Exercise 17.1: Acceleration in Simple Harmonic Motion

A particle undergoing simple harmonic motion along the x-axis has the position vector

$\vec r(t)=A\cos(\omega t) \hat x$ .

Let’s start with a quick review.

A. What are the units of $A$ and $\omega$ ? Combine these two constants so that the resulting combination has units of acceleration. This will be a characteristic acceleration for the problem.

B. You know how to compute $\vec v(t)$ given $\vec r(t)$ , and we just learned how to compute $\vec a(t)$ given $\vec v(t)$ . Find the acceleration vector $\vec a(t)$ for a particle undergoing simple harmonic motion as above.

C. Based on your answer to question 2, what is the physical interpretation for the combination of $A$ and $\omega$ you identified in question 1?

Exercise 17.2: Slingshot Physics

You probably have seen slingshot rides in amusement pars. Here’s a brief video of the slingshot ride at Cedar Point, in Michigan.

I used the video to time how long it takes for the people to go all the way up and all the way back down one time. That whole thing takes about 10 s. I also checked the Cedar Point’s website, which tells me that people are shot 110 m up in the air.

A. What is the maximum acceleration experienced by these people as they are shot upwards? (Hint: notice that they are just bouncing up and down! What kind of motion is that? You will also need to use the result from the previous problem.)

B. When you drop an object on the surface of the Earth, it falls with a constant acceleration of $9.8\ {\rm m/s}$ . We call this number $g$ , the acceleration on Earth. How many g’s is the maximum acceleration experienced by the folks in the video?

While acceleration is thrilling (as shown in the video!), too much acceleration can be deadly. For instance, without proper training, most people will pass out if they experience accelerations of $\approx 3g$ . How does this threshold compare to the acceleration you just found?

Exercise 17.3: Reading Changes in Velocity from Acceleration vs Time Graphs

Let’s make sure we are comfortable using this important fact to answer a few questions. These questions are all based on the four graphs below, which show acceleration vs time. In all cases, assume that the particle described by these graphs has zero velocity at $t=0$ .

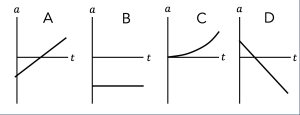
Key Takeaways

17 Acceleration Practice

License

Share This Book