Centripetal Acceleration

37 Centripetal Acceleration

So far, we have learned that for an object to move in uniform circular motion, it must be subject to a centripetal force. Since the object experiences a force pointing towards the center, it must also have a centripetal acceleration. Let’s set out to compute this centripetal acceleration.

Exercise 37.1: Centripetal Acceleration

Last chapter, we learned that the $x$ and $y$ coordinate of an object in circular motion can be thought of as simple harmonic motion.

Consider an object moving in uniform circular motion with angular velocity $\omega$ and $\theta=0$ at $t=0$ .

A. Write down the expressions for $x(t)$ and $y(t)$ for this particle.

B. Compute $\ddot x(t)$ and $\ddot y(t)$ . Use your result to determine how the acceleration vector $\vec a = \ddot x(t) \hat x +\ddot y(t) \hat y$ is related to the position vector $\vec r(t)= x(t)\hat x + y(t) \hat y$ .

If you haven’t run into this before, a “dot” means “take a derivative. Thus, $\dot x = dx/dt$ , while $\ddot x = d^2x/dt^2$ .

C. Calculate the magnitude of the acceleration vector, which we will denote $a_{\rm cen}$ . It is pretty standard to refer to this magnitude as the centripetal acceleration, even though technically acceleration needs to be a vector.

Rewrite your final answer both in terms of $\omega$ , and replacing $\omega$ in favor of $v_{\rm tan}$ .

D. Describe in English the direction of the acceleration vector. Is your answer consistent with Newton’s laws? Explain.

Bottom line:

The centripetal acceleration experienced by an object moving in uniform circular motion is $a_{\rm cen}=v_{\rm tan}^2/r$ .

This is an important results about physics that you should remember, so it goes in our tablets.

With an expression for the centripetal acceleration in hand, we are finally ready to apply Newton’s laws within the context of objections moving in a circle. Let’s give it a go.

Exercise 37.2: A ball on a string

Consider a string: if you pull on it hard enough, it will break. Let’s call the tension at which the string breaks $T_{\rm max}$ . Assume this string is tied to a tennis ball of mass $m$ . The length between one end of the string and the tennis ball is $L$ .

How fast can you spin the ball before the string breaks?

Now let’s do our drawing. Make sure it’s clear the tennis ball is moving in a circle.

Now find relations and solve. This is a force problem, so we start be setting up Newton’s laws. Remember you know what the acceleration of the tennis ball is! If you get stuck, you can look at my solution.

Exercise 37.3: Highway exit

Suppose you wanted to design a circular highway exit with a speed limit of 40 mph ( $\approx 18\ {\rm m/s}$ ). Even if the posted speed limit if 40 mph, you know there will be cars going faster, so let’s design that exit so that it can accommodate a car traveling up to 60 mph ( $\approx 27\ {\rm m/s}$ ) to be safe. A typical car tire has a static frictional coefficient $\mu=0.7$ .

Note: we will say more about friction for rolling objects like tires later in class. For now, I’ll just say that rolling doesn’t involve “rubbing.” Since there is no rubbing, there is no kinetic friction; despite its name, the relevant friction for rolling objects is static friction.

A. If the curve is too tight (i.e. the radius too small), a car exiting the highway will slip out and hit the barriers. What should the radius of the highway exit be to keep everyone safe?

You already know that when it rains you should slow down. Let’s see why. In the first part of the problem, you found the radius needed to keep a high way exit safe assuming that a car takes the exit at a speed of 60 mph. Water lubricates the road, so that the frictional coefficient of the tires decreases to $\mu\approx 0.4$ on a wet road.

B. How fast could you go in the highway exit you designed on a wet road without skidding out?

Key Takeaways

Optional: An Alternative Derivation of the Formula for Centripetal Acceleration.

Some people like geometry. If that’s you, here is an alternative derivation of the formula for centripetal acceleration using geometry. Let’s start with the setup.

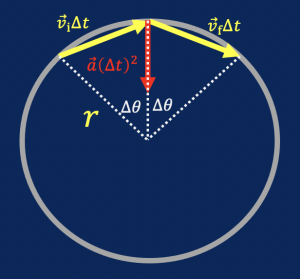The end result is the diagram show at right. Use this diagram to calculate the centripetal acceleration of an object moving with constant speed $v$ .

Note: this is not a physics problem, but a geometry problem. What is the length of the red arrow? You should also use the small angle approximation.

If you get stuck, you can find my solution below.

37 Centripetal Acceleration

Optional: An Alternative Derivation of the Formula for Centripetal Acceleration.

License

Share This Book