34 Radians Rule!
In the previous chapter, we learned that if I constantly push a particle in a direction that is perpendicular to its motion, the particle will end up moving in a circle. Before we start discussing how to mathematically describe circular motion, we should review two pieces of mathematics that we will need to use:
- Why you should always use radians.
- The small angle approximation.
We’ll do this as exercises to make sure we’re comfortable with these.
Exercise 34.1: How to measure angles
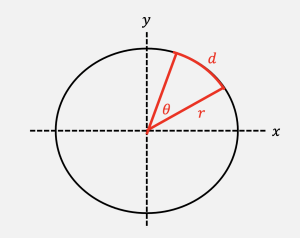 Take a circle, and draw two radii that make angle
Take a circle, and draw two radii that make angle ![]() as shown in the picture at right.
as shown in the picture at right.
A. Assume that ![]() is measured in degrees. Find an expression for the length of arc
is measured in degrees. Find an expression for the length of arc ![]() as a function of
as a function of ![]() .
.
B. Now repeat part A, but assume that ![]() is measured in radians.
is measured in radians.
C. Use your answer to explain why radians rule.
To a pretty good approximation, you should never use degrees when doing math. It will only bring you unnecessary pain and suffering. In fact, let me make this as clear as possible: to a very good approximation,
Every formula involving angles in every physics textbook in existence assumes angles are measured in radians.
Before moving on, let me dwell on a key piece of information you found in the previous problem: the arc length ![]() spanned by an angle
spanned by an angle ![]() in a circle of radius
in a circle of radius ![]() is
is
![]() .
.
This is a key relation we will use below a couple of times. I’m not adding it to our “physics tablets” because it’s not really about physics. Nevertheless, you must know this bit of math!
We now turn to the small angle approximation.
Exercise 34.2: The Small Angle Approximation
Prove that ![]() when
when ![]() is small.
is small.
Hint: Consider the approximation ![]() when
when ![]() is the sine function.
is the sine function.
There’s actually fun bit of math you can do with these type of Taylor series expansions. Specifically, you can use these expansions to come with interesting approximations for ![]() . If you’re intrigued, you can watch this next video just because it’s fun (definitely not required).
. If you’re intrigued, you can watch this next video just because it’s fun (definitely not required).
You will need both of these pieces of math in the coming chapters.
Key Takeaways
