2 Coordinate Systems
Our goal for this book is to be able to describe the motion of objects using math. This is the foundational skill that enables our modern world to exist. Our first step must be for us to learn how to describe the position of an object. We do this using a coordinate system. A coordinate system lays down a grid over the space we are interested in, with each point in the space getting assigned an “address.” Let’s go through this in the next video.
Let us quickly highlight the key points:
- When setting a coordinate system you are free to choose any point as the origin.
- The address for a point
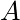is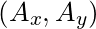 
. 
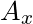is referred to as the x-coordinate, and 
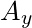is the y-coordinate. Starting from the origin:
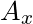- is the number of steps to the right/left we must take to get to .
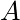- If 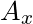is positive, we move right; if negative, then we move left instead.
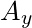- is the number of steps up/down we must take to get to .
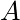- If 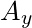is positive, we move up; if negative, then we move down instead.
Let’s try some quick exercises to make sure we’re all in the same page.
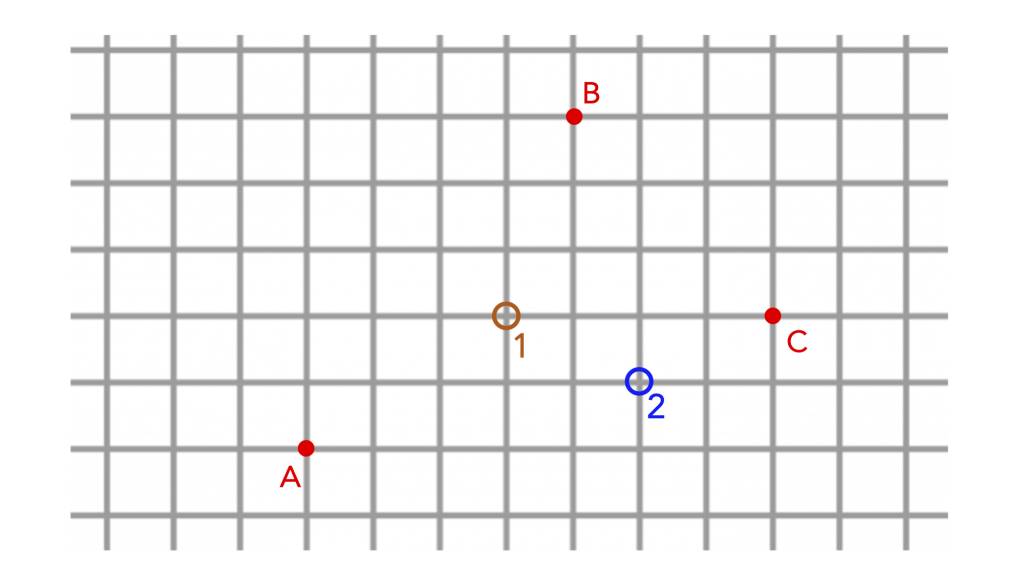
Exercise 2.1: Using Coordinate Systems
Point is 2 grids to the right of the origin, and 4 grid cells up from the origin. Assume each grid cell is 1 m in length.
Point 
is one grid cell to the left, and two grid cells down from the origin.
Exercise 2.2: Reading Positions from a Graph
The plot below shows two possible origins, labelled “1” (orange) and “2” (blue). What are the coordinates of Aisha, Beth, and Charlie for these two different origins? Assume that the grid uses units of meters, so that each grid cell is 1 meter to a side.
Key Takeaways
Given a coordinate system, a point that is grid cells to the right of the origin, and grid cells up from the origin, has coordinates .