40 Non-Constant Forces
We have studied motion under a constant force, and motion under a force that is constant in magnitude, and always perpendicular to the direction of motion (i.e. uniform circular motion). Let us consider now an arbitrary force 
.
Exercise 40.1: Motion from non-Constant Forces
Suppose an object is subject to a force which is known a priori.
A. Calculate the acceleration 
of this object.
B. Use your result to find an expression for the position 
and velocity 
of this object as a function of time. Assume the initial position and velocities are 
and 
at time 
.
This is pretty remarkable: if you tell me , I can tell you exactly how an object will move and where it will be at all times. Since we now know how to calculate the position vector of anything, that must mean we’re done, right?
Alas- not quite.
We have seen forces come about from one thing pushing on another. That is, the force between objects depend on their relative positions. This is a huge problems. Let’s see how.
Suppose I have two objects 
and 
that can interact:
- If I want to solve for
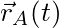, I need to know the force 
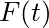that 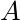experiences. - But- this force depends on where 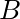. Thus, I need to know
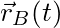. - To get 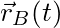I need to know the force that 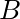experiences.
- But- the force 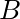experiences depends on 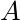, so I need to know .
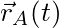You can see the problem. While we can, in principle, set up Newton’s laws for these objects, we can’t solve the equations. You can plug these equations into a computer, and then use the compute to move time forward. This is called a simulation. The video below shows one of these simulations in which physicists track billions of particles, brute-force integrating everything using a computer. The end result shows us how the matter in the Universe evolves, forming the galaxies we see today.
This is super-cool, but not the point of this book. Rather, we want to build some insight. To do so, we’ll need to get clever.