Displaced Oscillators

49 Displaced Oscillators

Let’s start with a warmup exercise.

Exercise 49.1: A Cart with a Spring

A spring of length $L$ is attached to the ceiling. You place a cart exactly below the spring. The top of the cart is an additional distance $L$ from the bottom of the hanging spring. You stretch the spring and hook up its free end to the cart, so that the spring pulls up on the cart. The spring is not strong enough to lift the cart from the floor. The floor is frictionless.

You then grab the cart, displace it horizontally a distance d along the floor, and let go. Find the cart’s position as a function of time.

Let’s walk through the solution together, starting with the story. Describe in English how the cart will move.

Now that you know what’s happening, let’s make a picture. Set $x=0$ to be the equilibrium position of the cart, and then find $F(x)$ . Use the approximation $\sqrt{L^2+x^2} \approx L$ when $x$ is small.

If you get stuck, look at my drawing and take it from there.

Now find relations. Start by using Newton’s law to find the relation between force and acceleration. You should find that it looks like $\ddot x = - ({\rm something})x$ .

You know what the most general solution to this differential equation is! Use the initial conditions to determine an expression for $x(t)$ .

D. Find the period of the oscillations.

Moving on. So far in this book we have looked at how objects move when: 1) subject to a constant force; and 2) subject to a linear force. But what about objects that are subject to both a constant force and a linear force? Let’s figure it out by looking at a specific example.

Exercise 49.2: Displaced Oscillators

Consider a spring that is hung from the ceiling. To the bottom end of the spring you attach a mass $m$ .

A. Define $y=0$ as the location of the end of the spring prior to hanging a mass from it. Find the distance $y_{\rm eq}$ that the spring stretches when the mass hangs in equilibrium.

B. You grab the block, raise it a distance $d$ , and let go. Describe in English what happens to the block.

Now that you know what should happen, let’s go about finding exactly how the block will move. Draw a picture of the mass hanging at some distance $\Delta y$ above the equilibrium point. If you get stuck, check to make sure your sketch matches mine.

Now find relations and solve: we need to figure out how the object moves, so we start with Newton’s laws. Remember to use that the acceleration is related to $\Delta y$ via $a=d^2(\Delta y)/dt^2$ .

There are two big takeaways from this problem.

An object subject to the sum of a constant force and a spring force will have an equilibrium point that is displaced from 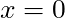$x=0$ (the unstretched spring).
If you displace this object from its new equilibrium, it will oscillate in simple harmonic motion with the same angular frequency $\omega^2=k/m$ .

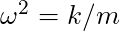If you want to prove this result in general, you can solve the extra problem at the end of this chapter. However, I’m more interested in you remembering these two points: if you do so, you can quickly solve “hard” problems by understanding things in English. Let me give you an example.

Exercise 49.3: Breaking Masses on Springs

A spring of constant $k$ hangs from the ceiling. The bottom of the spring has a mass $m$ attached to it. A second mass $m$ is glued at the bottom of the first mass. Suddenly, the glue fails, and the second mass $m$ drops.

Describe (in English!) the subsequent motion of the mass that remains attached to the spring.

B. Find the equation describing the motion of the mass that remains attached to the spring.

Key Takeaways

Extra Problems (Optional)

Optional Problem: Above, I asserted without proof that a linear plus constant force can be treated as a simple harmonic oscillator about its new equilibrium point. We explicitly saw an example of this, but we didn’t prove it in general. If you are interested, you can do so by solving the following problem. A mass $m$ is subject to a force $F=-kx+F_0$ .

A. Find the new equilibrium point $x_{\rm eq}$ .

B. Define $\tilde x = x-x_{\rm eq}$ . How does ${\dot {\tilde x}}$ compare to $\dot x$ ? Can you explain in English why this is the case?

C. How are ${\ddot {\tilde x}}$ and $\ddot x$ related?

D. Write Newton’s equation for $\tilde x$ , i.e. ${\ddot {\tilde x}} = {\rm something}$ . There should be no $x$ ‘s anywhere in your solution for the “something.” Use your result to argue that the object moves in simple harmonic motions about its equilibrium point $x_{\rm eq}$ .

49 Displaced Oscillators

Extra Problems (Optional)

License

Share This Book