Dot Products

51 Dot Products

Consider two vectors $\vec A$ and $\vec B$ . The dot product is defined as follows:

$\vec A \cdot \vec B = A_\parallel B$

where $A_\parallel$ is the component of the vector $\vec A$ which is parallel to vector $\vec B$ . Note that the dot product of two vectors is a scalar!

Exercise 51.1: Commutativity

Consider the diagram below. Find the dot products $\vec A \cdot \vec B$ and $\vec B\cdot \vec A$ in terms of the magnitudes $A$ and $B$ and the angle $\theta$ . Is it the case that the two products are equal to each other? If you get stuck, use the slider to see how I approach the problem.

The fact that $\vec A\cdot \vec B = \vec B \cdot \vec A$ means that dot products are commutative: the order of the products doesn’t change the answer.

Now- we found that the dot product can be written as $\vec A \cdot \vec B = AB\cos\theta$ . Most books use this formula as the definition of the dot product. However, I urge you NOT to memorize this equation. Let me show you why.

Exercise 51.2: Dot products pick out the parallel component

Compute the dot product $\vec A \cdot \vec B$ for the two cases shown in the diagram below.

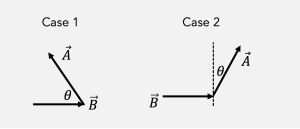
Let’s answer a few more questions about dot products to make sure we’re all on the same page.

Exercise 51.3: Properties of Dot Products

If you got any of these questions wrong, make sure you go back and figure out why the correct answer is what it is.

Let me stop here to point out that in the previous chapter, we figured out that if a force is parallel to the velocity, then the force will add kinetic energy. If the force is perpendicular to the velocity of an object, then it doesn’t add or subtract energy, whereas if the force is in the opposite direction as the velocity, then the force will subtract kinetic energy. Clearly, how much kinetic energy a force add or subtracts has something to do with the dot product $\vec F\cdot \vec v$ . We will get to that next chapter.

Moving on. Another thing you need to learn is how to compute the dot product of two vectors if you are given their components. Given the vectors $\vec A = (A_x,A_y,A_z)$ and $\vec B =(B_x,B_y,B_z)$ , the dot product $\vec A\cdot \vec B$ is given by

$\vec A\cdot \vec B = A_xB_x +A_yB_y +A_zBz$ .

Notice that if you take the dot product of a vector $\vec A$ with itself, you just get the magnitude squared to the vector, i.e.

$A^2 = \vec A\cdot \vec A = A_x^2+A_y^2 + A_z^2.$

Our components formula for the dot product $\vec A\cdot \vec B$ is pretty easy to remember. It also makes it obvious that $\vec A\cdot \vec B = \vec B \cdot \vec A$ . While I have not proven the above formula, I don’t find the proof particularly illuminating, so I will skip it (this is not a math textbook!). However, I will note that we could have adopted this formula as our definition, and then used it to prove that $\vec A \cdot \vec B = A_\parallel B$ . Let’s do so now.

Exercise 51.4: Dot Products Pick Out the Parallel Component

Use the equation for $\vec A \cdot \vec B$ in terms of components to prove that for any two vectors $\vec A$ and $\vec B$ , you can write the dot product as $\vec A \cdot \vec B = A_\parallel B$ .

You can also use our components expression to verify that dot products are “nice”: not only are they commutative ( $\vec A \cdot \vec B = \vec B \cdot \vec A$ ), they are also distributive (i.e. they slide past parenthesis).

Exercise 51.5: Dot Products are Distributive

Use the components expression for the dot product to prove that

$\vec A\cdot (\vec B +\vec C) = \vec A \cdot \vec B + \vec A \cdot \vec C$ .

The point here is that dot products basically behave like ordinary multiplication, so it’s easy to work with them.

Key Takeaways

51 Dot Products

License

Share This Book