28 Ropes
In chapter 25, we learned about the rule of touching: any two objects that “touch” exert a force on each other. This force is usually called the normal force, and it has to do with an object “pushing into” the other. However, as you well know, you can’t use ropes to “push” something: ropes pull.
Exercise 28.1: Tension
You are standing at the top of a building. A rope is attached to a pile of bricks. You pull on the rope to bring the bricks up at a constant speed.
The force of the rope on the bricks is called tension of the rope. Draw a qualitatively correct force diagram for the rope pulling on the bricks. Remember the bricks are coming up with constant speed.
Note that since the bricks are going with constant velocity, the net force on the bricks must be zero. Therefore, in the diagram ![]() and
and ![]() must have the same length.
must have the same length.
Important: the tension of a rope is, to a good approximation, the same throughout the entire rope. For instance, if you use a rope to pull up a bucket of bricks, you certainly feel the weight of bricks. However, it’s not the bricks pulling on your hands, it’s the rope! For this reason, you can think of ropes as “force transporters.” Bottom line:
The tension in a rope is constant.
This is not exactly true, but is usually a very good approximation, and so we will adopt it as our default in this book. If you are curious, I explain why the tension in a rope is roughly constant at the end of this chapter. For now, let’s do a couple of problems to get some practice.
Exercise 28.2: Pulling up bricks
You are lifting a pile of bricks at constant velocity as shown in the picture below. The bricks have mass ![]() , while you have mass
, while you have mass ![]() . Determine how hard the floor is pushing up on you.
. Determine how hard the floor is pushing up on you.
Exercise 28.3: Pulling two boxes
A box of mass ![]() is attached to a box of mass
is attached to a box of mass ![]() by a rope. Both boxes rest on a frictionless surface. The box of mass
by a rope. Both boxes rest on a frictionless surface. The box of mass ![]() has a second rope attached to it. You grab the rope, and pull it with force
has a second rope attached to it. You grab the rope, and pull it with force ![]() , accelerating the boxes to the right.
, accelerating the boxes to the right.
Find how fast the boxes are moving after a time ![]() .
.
Before moving on, here is a nice alternative way of solving the problem above. Looking at our picture, we can see both boxes move together. Therefore, we can think of the two boxes as a single “thing” of mass ![]() . The acceleration of the “thing” when pulled by a force
. The acceleration of the “thing” when pulled by a force ![]() is given by Newton’s law:
is given by Newton’s law: ![]() .
.
You will occasionally run into problems like this one, where “joining” multiple objects into one “thing” is useful, so it’s worth knowing this trick. To sound scientific, rather than talking about “things,” physicists usually used the word system, as in “consider the force applied to the system comprised of the two boxes joined with the rope.” See how fancy it sounds?
Exercise 28.4: One more time, with friction!
Consider the setup from problem 22.3: two boxes attached with a rope, and you pulled on the larger box with force ![]() . This time, however, there is friction between boxes and the floor. The kinetic and static frictional coefficients are
. This time, however, there is friction between boxes and the floor. The kinetic and static frictional coefficients are ![]() and
and ![]() respectively. How hard should you pull on the rope to keep the boxes moving at constant velocity?
respectively. How hard should you pull on the rope to keep the boxes moving at constant velocity?
Hint: consider the system comprised of the two boxes.
To end, I would like to solve one more problem which I think is kind of cool. Before we do that, I want to review how we can use calculus to find the maximum/minimum of a function. If you’re comfortable with that, you can skip the green box below.
Calculus: Finding Minima and Maxima
Suppose we wanted to find the maxima of a function ![]() . We know that the derivative
. We know that the derivative ![]() is the slope of that function. Thus, if
is the slope of that function. Thus, if ![]() is not zero, we can’t possibly be at a maximum: if we climb up the slope, we’ll be higher. Consequently,
is not zero, we can’t possibly be at a maximum: if we climb up the slope, we’ll be higher. Consequently,
If the function ![]() has a maximum at position
has a maximum at position ![]() , then
, then ![]() .
.
Of course, the same is true for minima: if ![]() , we can climb down to get to a lower value.
, we can climb down to get to a lower value.
This means that if we want to find a maximum/minimum, we can just find the points where ![]() , and then check whether those points are maxima/minima or not. Note it is not sufficient for
, and then check whether those points are maxima/minima or not. Note it is not sufficient for ![]() to be zero. For instance,
to be zero. For instance, ![]() has
has ![]() , but the point
, but the point ![]() is neither a maximum nor a minimum.
is neither a maximum nor a minimum.
Exercise 28.5:
A rope is attached to a big heavy box of mass ![]() . You are asked to pull on the rope to slide the box across the room. Being lazy, you decide to figure out at what angle
. You are asked to pull on the rope to slide the box across the room. Being lazy, you decide to figure out at what angle ![]() you should pull to minimize the force needed to keep the box moving (see picture below, but don’t use the slider yet!).
you should pull to minimize the force needed to keep the box moving (see picture below, but don’t use the slider yet!).
A. Naively, one might think that you can minimize the force by pulling horizontally. This is not correct. Explain why. Hint: the real world has friction!
B. Find the force ![]() that must be applied to move the box with constant velocity as a function of the angle
that must be applied to move the box with constant velocity as a function of the angle ![]() .
.
If you get stuck, start by checking that your force diagram agrees with mine (use the slider above). If it doesn’t, fix it, and then finish the problem on your own. You can go over my solution below.
C. With ![]() in hand, find the value of
in hand, find the value of ![]() which minimizes the force
which minimizes the force ![]() .
.
Key Takeaways
Optional: Why are ropes “force transporters”?
Consider a long rope, such as the one shown in the picture below. The rope has a linear mass density ![]() , where
, where ![]() is the mass of the rope, and
is the mass of the rope, and ![]() is the rope’s length.
is the rope’s length.
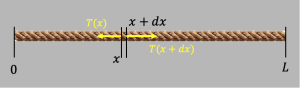
Let ![]() denote the variable that tells us how far we are from the left end of the rope, and consider an infinitesimally small part of the rope between positions
denote the variable that tells us how far we are from the left end of the rope, and consider an infinitesimally small part of the rope between positions ![]() and
and ![]() . We will let
. We will let ![]() be the tension of the rope as a function of
be the tension of the rope as a function of ![]() . We will further assume that the rope as a whole is moving together to the right with acceleration
. We will further assume that the rope as a whole is moving together to the right with acceleration ![]() .
.
Let us write Newton’s second law for that little piece of rope between ![]() and
and ![]() . This little piece of rope has a mass
. This little piece of rope has a mass ![]() . It gets pulled to the right with force
. It gets pulled to the right with force ![]() , and it gets pulled to the left with force
, and it gets pulled to the left with force ![]() . We have then
. We have then
![]() .
.
But we also know that the left hand side of the equation is equal to ![]() , where
, where ![]() is the derivative of
is the derivative of ![]() . Plugging in, and cancelling the
. Plugging in, and cancelling the ![]() , we arrive at
, we arrive at ![]() . We can readily integrate this equation to find
. We can readily integrate this equation to find ![]() :
:
![]()
or simply ![]() .
.
There are several things to note here. First: if the rope is not accelerating, then ![]() , i.e. the rope is a force transporter! However, if the rope is accelerating, the two ends of the rope will be at somewhat different tensions. This makes sense: if the rope is accelerating, there needs to be a non-zero net force acting on it! However, if the mass of is rope is small, and the tension is large, then
, i.e. the rope is a force transporter! However, if the rope is accelerating, the two ends of the rope will be at somewhat different tensions. This makes sense: if the rope is accelerating, there needs to be a non-zero net force acting on it! However, if the mass of is rope is small, and the tension is large, then ![]() , and we end up with
, and we end up with ![]() everywhere.
everywhere.
That is to say, the tension in a rope is not exactly constant if the rope is accelerating, but as long as the rope’s mass is small, setting the tension to a constant will be a good approximation.
