How to Use the Center of Mass

63 How to Use the Center of Mass

Last chapter, we learned that

The center of mass of a system moves as though it is a single particle of mass $m_{\rm tot}$ that is subject to the total external force $\vec F_{\rm ext}$ .

You know this is a big deal because I’ve said several times now. Before we get to how we can use this result to solve problems, let’s make sure we are comfortable calculating the center of mass of a system.

Exercise 43.1: Center of Mass

A. Consider the Earth and the Sun. Their mass are $m_{\rm E}=6.0\times 10^{24}\ {\rm kg}$ and $m_{\rm S}=2.0\times 10^{30}\ {\rm kg}$ . The distance from the Sun to the Earth is $d=1.5\times 10^8\ {\rm km}$ . Calculate the distance from the Sun to the center of mass of the Earth–Sun system.

For reference, the radius of the Sun is $R_\odot = 7.0\times 10^5\ {\rm km}$ . Is the center of mass of the Earth–Sun system inside the Sun, or outside the Sun?

B. The most massive planet in the Solar System is Jupiter, which has a mass of $M_{\rm J}=1.9\times 10^{27}\ {\rm kg}$ , and is at a distance $d_{\rm J}=7.8\times 10^8\ {\rm km}$ from the Sun. What is the distance from the Sun to the center of mass of the Sun–Jupiter system?

Let’s do one more to illustrate an important feature of the center of mass.

Exercise 43.2: Center of Mass II

Consider a rectangle. The lower-left hand corner of the rectangle is at $(0,0)$ , the lower-right hand corner is at $(a,0)$ , and the upper-left hand corner is at $(0,b)$ .

A. Assume that there is a mass $m$ at each corner of the rectangle. Sketch the rectangle, and then find the position of the center of mass. Add the center of mass position to your drawing, and describe this position using one sentence in English.

If you need help with your sketch, you can see mine below.

B. Suppose that the masses on the right hand side of the rectangle are doubled, so they are now $2m$ . Find the new position of the center of mass. Did the center of mass move right or left? What about up/down? Does that make sense?

The point of this problem is this: when you are given a nicely symmetric mass distribution (e.g. a rectangle, or a circle), the center of mass of that mass distribution will coincide with the geometrical center. This makes it so you can easily determine the center of mass of many objects by eye, without having to do a bunch of math. Bottom line:

The center of mass of symmetric mass distributions coincides with the geometric center.

There is one additional nice property of a center of mass, namely, you can “chunk it.” Here’s what I mean: suppose we have two systems A and B. The center of mass A is $\vec r_{\rm A}$ , and the center of mass of B is $\vec r_{\rm B}$ . The center of mass of the joint A+B can be computed by pretending all of the mass of A is at $\vec r_{\rm A}$ , and all of the mass of B is at $\vec r_{\rm B}.$ . Let’s prove it

Exercise 43.3: Center of Mass Calculations are “Chunkable”

System A is comprised of $N$ particles, and system B is comprised of $N'$ particles. Show that

$\vec r_{\rm A+B} = \frac{ m_{\rm A}\vec r_{\rm A} + m_{\rm B} \vec r_{\rm B} }{m_{\rm A}+m_{\rm B}}$

where $\vec r$ is the center of mass of the system.

Hint: you may find it helpful to use different notation for A and B particles, e.g. $m$ and $\vec r$ for particles in system A, and $M$ and $\vec R$ for particles in system B.

Summarize your result as a single sentence in English.

Bottom line: given two systems A and B,

To calculate the center of mass of A+B you can pretend all of the mass on A is at the center of mass of A, and all of the mass of B is at the center of mass of B.

Let’s use this to calculate the center of mass of a “T”.

Exercise 43.4: Center of Mass of a Cross

Consider 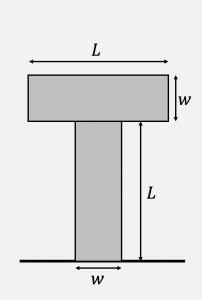the picture of the “T” shown at right. The “base” and the “cross bar” of the T each have a mass $m$ , length $L$ , and width $d$ . Calculate the position of the center of mass.

Let’s try doing some problems involving center of mass.

Exercise 43.3: What’s the Weight?

Imagine 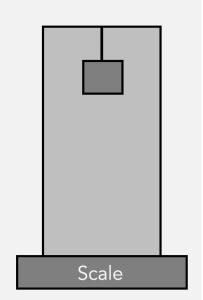you have a very large box sitting on very large, very accurate balance scale. The large box has a small but heavy box inside hanging from its “ceiling,” as shown in the picture at right. The scale marks that the weight of the large box and anything insider is $W$ .

Suppose that you are asked to keep an eye on the balance reader. While you are looking at the balance, the rope inside the large box snaps, and the small heavy box starts falling to the ground. Would you be able to tell that the rope broke just from looking at the scale? Explain your answer.

I am purposely not giving you the answer on this question as an invitation for you to ask other people and discuss the situation. However, here is a hint. Think about:

The external force acting on the system.
What the center of mass is doing before/after the rope breaks.

As it turns out, you can also use the center of mass as a “conservation law” under certain conditions. Let’s take a look.

Exercise 43.4: Walking on a Canoe

A man of mass $m$ is standing on the left edge of a canoe of mass $M$ and length $L$ . The man proceeds to walk from the left end of the canoe to the right end of the canoe. You can assume that the canoe in the water behaves as though it were resting on a frictionless surface.

As the man walks from the left end to the right end of the canoe, what happens to the canoe? Does the canoe move left, right, or stay in place? Justify your answer. If you think the canoe moves, determine the total distance the canoe moves.

This problem is hard if you haven’t run into something like this before, so I’ll help you out.

Step 0- What’s the story? This is before and after problem, but it’s a bit odd: the initial and final momentum are zero, so conservation of momentum doesn’t help. Let’s try something else.

How are the initial and final positions of the center of mass of the “canoe+man” system relate to each other? Justify your answer.

Step 1- Draw a picture. Draw the before an after picture. Make sure that it is easy to compare the positions of the canoe in the before and after picture, and clearly mark the origin. You can compare your picture to mine to make sure you got it.

Hint: the canoe moves along the x-axis. We will want to clearly show how things move, so it’s best to make the before/after pictures be one on top of the other, so that can clearly see how things have moved from the “before” to the “after.”

Steps 2 and 3- Find relations and solve. In step 0, we figured out that the center of mass of the system doesn’t change. Set $x_{\rm com,i}=x_{\rm com,f}$ , and solve for the position of the canoe.

63 How to Use the Center of Mass

License

Share This Book