29 Practice Makes Perfect I

A daredevil wants to jump from one ramp to another.  Each ramp is big, reaching a height h, and making an angle with the horizontal.  To make the jump, he straps a rocket to his motorcycle.  When lit, the rocket pushes on the motorcycle with a known force given by rocket’s manufacturer.   The mass of the daredevil plus the mass of the motorcycle is .  The rocket has negligible mass.  The daredevil starts at the bottom of the ramp, and lights the rocket.  As soon as he reaches the top of the launching ramp, he ditches the rocket, so he is on free fall from that point on.

Determine how far should the two ramps be from each other in order for the daredevil to just barely reach the second ramp.  You can ignore friction between the motorcycle wheels and the ramps.

If you get stuck, make sure your diagram agrees with mine.  If you’re still stuck, you can check out the hint.

I’ve split the answer in two.  That way, if you need to the look up the solution, you can go through the first half, and then try your hand at finishing the problem by yourself.

Of course, in practice, people don’t strap rockets to their bikes: they just make sure that they leave the ramp at the appropriate velocity necessitated by the jump.  Still- the whole thing can look really impressive.

On July 17, 1981, the walkway of the Hyatt Regency Kansas City Hotel collapsed. 114 people were killed, and an additional 216 were hurt. The Hyatt Regency collapse remains to this date the deadliest non-deliberate structural failure in American history.

The hotel walkways were designed to hang one top of the other from a single set of rods. During construction, the builder requested to “split” the rods, as shown in the diagram below.  The request was approved without a thorough analysis, which resulted in the collapse of the two walkways.

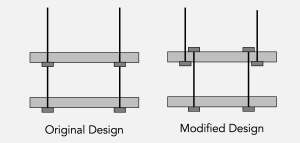
The point of failure in the Hyatt Regency disaster were the nuts used to secure the walkways: if the force on a nut is too large, the nut will fail, and the walkways collapse.

Draw the force diagram for each of the two walkways. Set up Newton’s equations, and compare the force acting on the nuts of the upper walkway in each of the two designs.  Use your results to explain why the modified design resulted in the collapse of the walkways.

Grady from the youtube channel Practical Engineering has a fantastic video about the disaster, which I encourage you to watch (it’s really interesting!).

The elevators in the Shanghai tower are (at the time of writing) the fastest elevators in the world.  They rise for in a mere .

One way to build these elevators would be to try to get the elevator moving as fast as possible, then have the elevator move at some top speed for a long time, and then stop it as quickly as possible.  However, people usually don’t like being shot from a cannon straight at big, immovable wall.

How should the elevator move in order for the passengers to exhibit a relatively low acceleration, while still making the trip go quickly?

Assume you design the elevators in the Shanghai tower according to your plan above to determine the elevator’s top speed.

Try going through the four steps of problem solving to find the elevator’s top speed.  If you get stuck, check that your story matches mine.  Once you nail the story, make sure your picture matches mine.

I should say that real elevators are not designed to accelerate in quite this way.  While the general principle above is sound, notice that halfway through the ride our elevator goes from accelerating upwards to accelerating downwards.  This change will result in a big jerk, making the ride uncomfortable.  Thus, in practice, elevators “smooth out” that transition to ensure a comfortable ride.  This explains why our answer above and the maximum speed reported online are somewhat different.