Work from Non-Conservative Forces

58 Work from Non-Conservative Forces

Last chapter we derived the general form of the conservation of energy equation

$E_{\rm f} = E_{\rm i} + W_{\rm noncon}$ .

Here, $W_{\rm noncon}$ is the work done by non-conservative forces, i.e. forces that don’t have a potential energy. In our studies so far we have run into three forces for which we have no potential energy: friction, the normal force, and tension. We’re going to go through each in turn. First up, friction.

Exercise 58.1: Work Done by Friction

In other words, friction drinks energy. At least usually! Sometimes, it can go the other way:

Exercise 58.2: Friction can add energy

So- friction usually drinks energy, but it can be complicated. Let’s make sure we’re comfortable with doing calculations involving friction by solving a problem.

Exercise 58.3: A sliding block

A block of mass $m$ is slid up a ramp. The ramp make an angle $\theta$ with the horizontal. The block and ramp have a frictional coefficient $\mu(x)=\mu_0x$ , where $\mu_0$ is a constant, and $x$ is the distance along the ramp, starting from the bottom of the ramp. You slide the block upwards with an initial speed $v_0$ from the bottom of the ramp.

Find how far the block travels along the ramp.

Step 0- what’s the story? Is this a before and after problem? When does it start? When does it end? How are we going to solve the problem?

Step 1- draw a picture.

Steps 2 and 3- find relations and solve.

Now let’s think about the normal force.

Exercise 58.4: The Normal Force

Consider an object moving along the floor. Is the work done by the normal force positive, negative, or zero? Justify your answer.

So- the work done by the normal force is usually zero. But not always. Here’s an example: you throw a wad of wet toilet paper at a wall. Evidently, before the collision the paper had kinetic energy, and after the collision, it didn’t. The reason: the normal force between the toilet paper and the wall did work. Explain how that is possible.

This is pretty similar to what we saw with a bouncing ball. Consider the bouncing ball at right. When the ball first touches the floor, it starts getting squished: the ball is moving down, but the floor is clearly pushing up: the normal force from the floor is doing work on the ball, removing energy. This makes sense: the floor is stopping the ball. As the ball starts to bounce up, the floor is still pushing up, but now the ball is starting to move up: the normal force does positive work. For a rubber ball, the net positive work will be (roughly) equal to the net negative work, so that the net work done is zero. For wet toilet paper, there is no “second half of the bounce”, and therefore we end up with the normal force doing negative work.

So, friction usually drinks energy, but not always. Likewise, the normal force usually does no work, but not always. What about the tension force?

Exercise 58.5: Tension

Consider 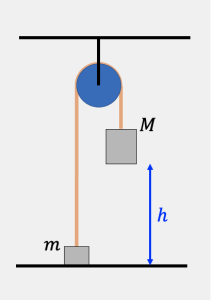a rope that is attached to an object on either end. As a specific example, consider Atwood’s machine shown at right. As usual, the big mass starts falling down, while the small mass starts accelerating upwards.

A. As the big mass moves down, is the work done by the tension force on the big mass positive or negative?

B. As the small mass moves up, is the work done by the tension force on the small mass positive or negative?

C. Which of the two works above is bigger in magnitude: the work of the tension force on the big mass, or the work of the tension force on the small mass. Justify your answer.

D. Calculate the work done by the tension force on the system comprised of the two masses $m$ and $M$ . Justify your answer.

You can see that so long as we are interested in the total work done by the tension (including both boxes!), the total work done by the tension force is zero. This is usually what we’re interested in, so the work done by tension is usually zero. But not always! If we had asked about the work done by tension on the big box only, that work is negative. On the small box only, that works is positive.

We went through excruciating detail over the work being done by the tension force not because this is so special and unique, but because being comfortable with this can help us solve problems very quickly. In fact, let’s revisit the Atwood machine one more time.

Exercise 58.6: The Atwood Machine, Again!

Consider the Atwood machine at right. Find how high the small block will go.

I have broken the solution into many chunks: if you get stuck, you can look at the first part of the solution, and then try to do the rest. If you get stuck again, look at the next part, but then try to finish it up. And so on. The point here is to get practice solving problems.

Compare the initial potential energy of the large mass to the final potential energy of the small mass. Which is bigger? If you find one is bigger, explain exactly where energy was gained or lost. If you find they are the same, explain why they need to be the same.

So what is the bottom line from this chapter? Whether non-conservative forces do work, and what sign that work has, depends on the details of the problem. Indeed, it is precisely because the work done depends on the details of the problem that we can’t just simplify the whole thing in terms of a potential energy, like we did with gravity and springs. When it comes to non-conservative forces, you just need to think through them on a case-by-case basis. There is no shortcut.

Key Takeaways

58 Work from Non-Conservative Forces

License

Share This Book