Practice Makes Perfect IX

59 Practice Makes Perfect IX

In chapter 56 we derived the general form of the conservation of energy equation

$E_{\rm f} = E_{\rm i} + W_{\rm noncon}$ .

Here, $W_{\rm noncon}$ is the work done by non-conservative force, i.e. forces that don’t have a potential energy. We then spent a bunch of time in chapter 57 thinking about this term. Let’s make a quick inventory of forces with and without potential energy:

This chapter is about getting lots of practice solving problems using the conservation of energy equation. Some rules to live by:

Start be figuring out if there are multiple mini-stories.
Solve “before-and-after” mini-stories using conservation laws.
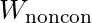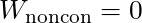When using conservation of energy, you always need to calculate $W_{\rm noncon}$ . If $W_{\rm noncon}=0$ , say so, and explain your reasoning. Don’t just ignore the term.

Exercise 59.1: Spring Gun

A spring with spring constant $k$ is attached to a wall. The other end is attached to a mass that rests on a frictionless table. You push on the mass and compress the spring a distance $d$ , and let go. The mass shoots out. It travels a distance $L$ , and then starts climbing up a frictionless ramp that makes an angle $\theta$ with the horizontal. Find the distance $D$ that the block travels along the ramp.

Suppose now that the block has a frictional coefficient $\mu$ with the floor and the ramp. How far would the block go then?

Exercise 59.2: The loop-the-loop

You want to make a toy track for your car such that your car makes a loop-the-loop. The radius of the loop is $R$ , and the car will roll down an incline starting at height $h$ before getting to the loop. What should the initial height $h$ of the toy car be in order for the car to make it all the way around the loop?

Ideally, you should be able to solve this problem on your own, without looking at anything of what I wrote below. If you need help, however, I’ve broken things down so you can try solving as much of the problem as you can do so on your own.

Exercise 59.3: Mass onto a spring

A spring of spring constant $k$ rests on a table. One end of the spring is attached to a wall, while the other end has a large block of mass $M$ . A small block of mass $m$ starts a distance $L$ from the free end of the spring. The small mass is slid towards the spring with an initial velocity $v_0$ . The static and frictional coefficients of all the blocks are identical, call them $\mu$ .

A. Find the minimum velocity $v_{\rm min}$ with which you must slide the small block in order for it to reach the big block.

B. We will assume that the block $M$ is sticky, so that if you slide the block $m$ with an initial speed $v_0 > v_{\rm min}$ , then the small block will stick to the big block. Clearly, the two blocks will then then be moving to the left, and will start to contract the spring. Find how much the spring is contracted at maximum compression. Note that the blocks are still sliding on the “friction-full” table as it is compressing the spring.

To solve this problem, you should start by identifying how many mini-stories there are. Make sure you know where each mini-story starts and ends, and how you should solve each mini-story.

If you’re feeling wobbly, here is a video where I talk through the story of the problem.

Now that we know we have 3 mini-stories, let’s draw a picture. The story should show the beginning and end of every mini-story! Note that stories 1 and 3 involve energy, so you should have a force diagram showing the forces involved during stories 1 and 3.

We are finally ready to solve the problem. Try solving each mini-story in turn. I include below a video solution for each mini-story. By the end, we will have our full solution.

Mini-story no: 1

Mini-story no. 2:

Mini-story no. 3:

C. If you slide the block with an initial speed $v_0=v_{\rm min}$ , the block will just barely touch the spring. Suppose that you slide the block with an initial speed that is just a tiny bit larger than $v_{\rm min}$ , so that the two blocks collide, and the spring gets compressed a bit. Will the blocks bounce back after maximum compression or not? Explain in English.

Exercise 59.4: The Ballistic Pendulum

A pendulum of mass $M$ is hanging from a nail attached to the wall. The length of the chord is $L$ . You shoot a bullet of mass $m$ towards the pendulum. The bullet strikes the pendulum horizontally with an initial velocity $v_0$ . Afterwards, the bullet becomes embedded in the pendulum, and the whole thing starts going up in a circle. What is the minimum speed $v_{\rm min}$ with which the bullet must be traveling for the pendulum to make it all the way around in a circle?

As before, try solving this problem without using anything of what I wrote below, but by all means go through this if you get stuck.

59 Practice Makes Perfect IX

License

Share This Book