12 Reading Displacement from Velocity Graphs
We have learned that displacement is the integral of velocity, i.e.
.
This result, along with our knowledge of calculus, allows us to “read off” the total displacement of a particle given a graph of its position versus time along any given dimension. The key fact we need is that the integral of a function can be thought of as “the area under the graph.” If you don’t quite remember where this comes from, go through the material in the “calculus review” box below.
Calculus- The integral of a function gives you the area under the graph
Consider some arbitrary function 
. In the video below, we demonstrate that the integral of gives us the area under the curve.
For our purposes, the important thing is that the displacement is the integral of velocity over time. That is,
The displacement of a particle is equal to the area under the curve of a graph of 
vs. 
.
Note that in general, 
is a vector quantity, so this is really a statement about the displacement along each component. That is, along the 
-axis, the displacement is the area under the curve of 
vs . Likewise, the area under the curve of 
vs is the displacement along the 
-axis. Let’s try using this to solve a couple of problems.
Exercise 12.1: Reading Displacement from Velocity vs Time Graphs
Consider the graphs below. Click on the appropriate description of the total displacement of experienced by a particle between 
and the last time shown in the graph. In all cases, you can assume the particle is only moving along the axis.
Let’s try this again for another set of graphs.
Let’s try one last series of questions based on one graph.
Exercise 12.2: Practice with Velocity vs. Time Graphs
The velocity of a car along a long, straight road is described by the graph below. Use the graph to answer the following series of questions.
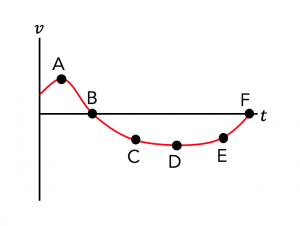
Describe in English the motion of this car.
Key Takeaways