4 Vector Addition
The great thing about vectors is that we can add them. Let’s see how this works:
Exercise 4.1: Vector Addition
You are given two displacement vectors 
and 
.
We want to define 
such that 
. What do you think are the components 
and 
?
Let’s think about what this mean in English. Consider the displacement vector
= “follow 
and then follow 
.”
Reason what the quantities and that describe the vector should be in terms of the components of and . Justify your answer in English.
There are several things to highlight from the above discussion. First,
To add vectors, we just need to add the components.
In other words, 
. This is pretty much the only thing you can write that makes sense, so it’s easy to remember!
The second thing to take away is that
When adding vectors, the “+” sign means “and then.”
In English, the equation 
means “Follow and then follow .” This brings me to my last point::
In physics, every equation is also an English sentence!
In other words, physics is not about equations, but rather understanding what those equations are saying: math is a tool, but understanding happens in English.
This understanding allows us to figure out how to graphically add vectors as well, as we now show.
Exercise 4.2: Adding Vectors Graphically.
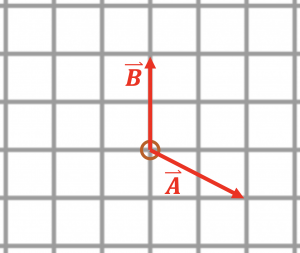Consider the diagram to the right. Find the vector where .
Do not use components! Try solving this problem by drawing a picture instead. Remember, the vector is found by following , and then following .
If you’re not sure how to get started, take a look at the solution video below. You’ll get a few more chances to practice after watching the video.
Solution:
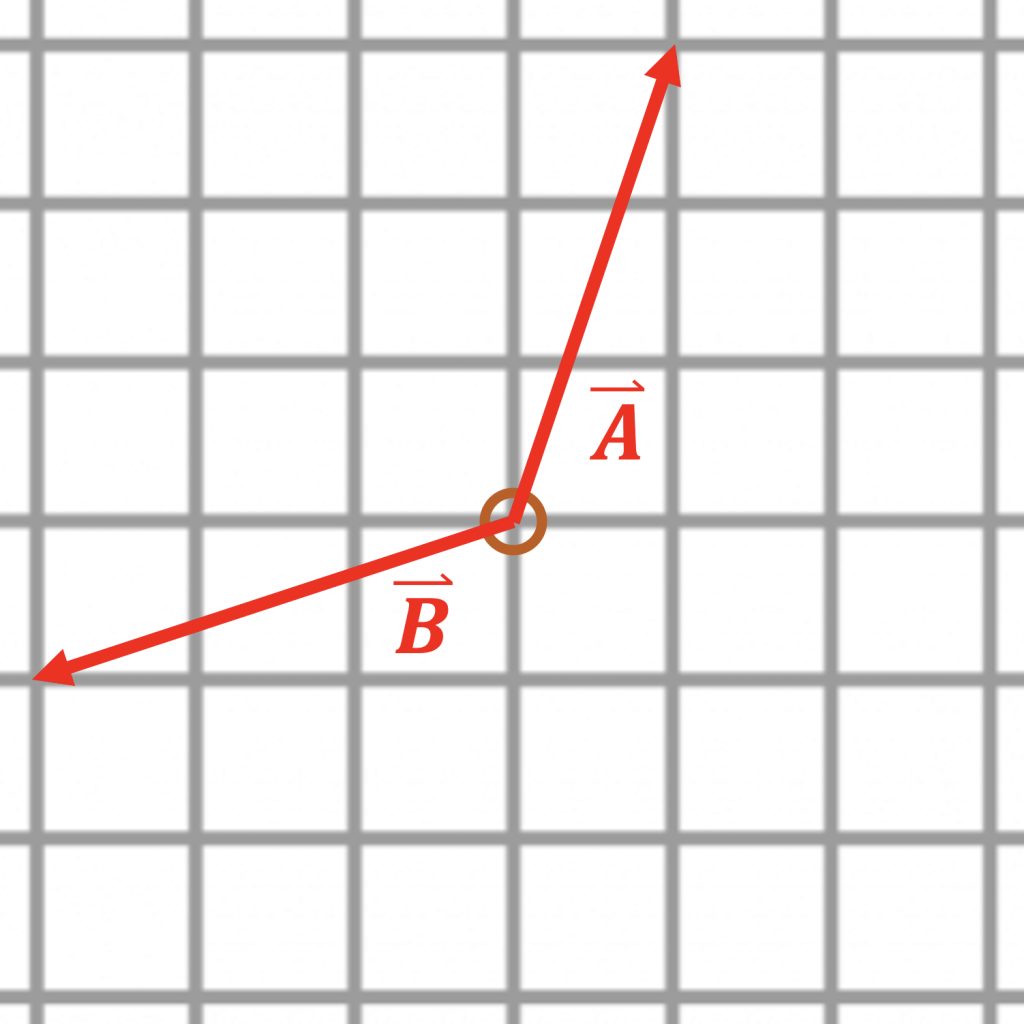
Exercise 4.3: Practice Vector Addition
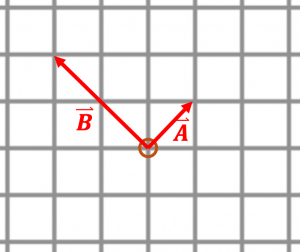
Exercise 4.4: Practice Vector Addition
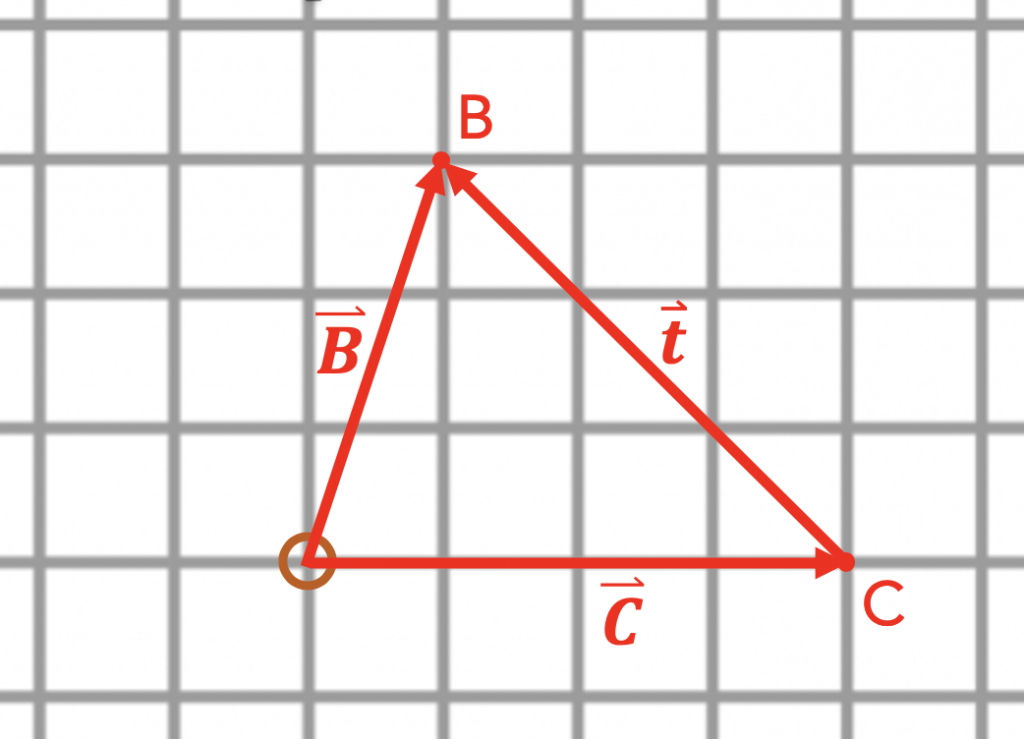
Exercise 4.5: Equations are Sentences!
I mentioned that in physics all equations should be thought of as sentences in English. Let’s drive this point home.
In the diagram below, you are standing at the origin (brown circle). Your two friends Charlie (C) and Beth (B) are nearby.
Key Takeaways